题目内容
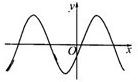
已知直线y=kx(k>0)与函数y=|sinx|的图象在[0,2π]上恰好有三个交点,从左到右依次记为O,B,C,设点C的横坐标为x0,则
|sinx|dx=( )
| ∫ | x0 0 |
分析:画出图象分析,可以看出:x0∈(π,
),且满足直线y=kx与函数y=|sinx|的图象相切,通过求导可求出斜率k,进一步可得出x0满足的关系式,据此可计算出答案.
| 3π |
| 2 |
解答:解:画出图象分析,可以看出:x0∈(π,
),且满足直线y=kx与函数y=|sinx|的图象相切,
∴-x0cosx0=-sinx0,即x0=tanx0<0,可得cosx0=-
.
∴
|sinx|dx=
sinxdx+
(-sinx)dx=(-cosx)
+cosx
=2+cosx0-(-1)=3-
.
故选A.
| 3π |
| 2 |
∴-x0cosx0=-sinx0,即x0=tanx0<0,可得cosx0=-
| 1 | ||||
|
∴
| ∫ | x0 0 |
| ∫ | π 0 |
| ∫ | x0 π |
| | | π 0 |
| | | x0 π |
| 1 | ||||
|
故选A.
点评:本题考查分区间求定积分,由题意找出x0的范围和具有的性质是解决问题的关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 已知直线y=kx(k>0)与函数y=2sin(x-
已知直线y=kx(k>0)与函数y=2sin(x-| π |
| 6 |
A、tan(α-
| ||
B、tan(β-
| ||
C、tan(α-
| ||
D、tan(β-
|