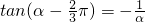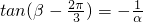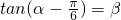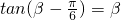题目内容
(实)已知直线y=kx(k>0)与函数y=2sin(x-
)的图象有且仅有两个公共点,若这两个公共点的横坐标分别为α,β,且β<α,则下列结论中正确的是( )
| π |
| 6 |
分析:利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率,最后将切点的坐标代入切线方程结合诱导公式即可使问题解决.
解答:解:令f(x)=2sin(x-
),
∵直线y=kx(k>0)从y轴开始围绕原点顺时针方向转动,y=kx(k>0)与函数y=2sin(x-
)的图象有一个交点,到相切时有两个公共点,再转下去会有超过两个的公共点.
∴直线y=kx(k>0)与函数y=2sin(x-
)的图象相切,
∴y′=2cos(x-
),即k=2cos(x-
),
∵直线y=kx(k>0)与函数y=2sin(x-
)的图象有且仅有两个公共点A,B,这两个公共点的横坐标分别为α,β,且β<α,故切点A(α,f(α)),交点B(β,f(β)),
所以切线方程为y=2xcos(α-
).
将切点的坐标(α,2sin(α-
))代入切线方程得:2sin(α-
)=2α•cos(α-
).
∴tan(α-
)=α.
∴tan(α-
)=tan[(α-
)-
]=-tan[
-(α-
)]=-
=-
.
故选A.
| π |
| 6 |
∵直线y=kx(k>0)从y轴开始围绕原点顺时针方向转动,y=kx(k>0)与函数y=2sin(x-
| π |
| 6 |
∴直线y=kx(k>0)与函数y=2sin(x-
| π |
| 6 |
∴y′=2cos(x-
| π |
| 6 |
| π |
| 6 |
∵直线y=kx(k>0)与函数y=2sin(x-
| π |
| 6 |
所以切线方程为y=2xcos(α-
| π |
| 6 |
将切点的坐标(α,2sin(α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴tan(α-
| π |
| 6 |
∴tan(α-
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 1 | ||
tan(α-
|
| 1 |
| α |
故选A.
点评:本小题主要考查正弦函数的图象,突出考查导数的几何意义、利用导数研究曲线上某点切线方程及三角函数的诱导公式等基础知识,属于难题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
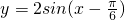 的图象有且仅有两个公共点,若这两个公共点的横坐标分别为α,β,且β<α,则下列结论中正确的是
的图象有且仅有两个公共点,若这两个公共点的横坐标分别为α,β,且β<α,则下列结论中正确的是