题目内容
(理)已知函数 若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
【答案】分析:根据题意,在坐标系里作出函数的图象,将直线y=y进行平行移动,可得左边两个交点关于直线x= 对称,故a+b=1,再观察对数函数图象得c满足1<c<2011,才能使两个图象有三个公共点,最后综合以上两点,可得出a+b+c的取值范围.
对称,故a+b=1,再观察对数函数图象得c满足1<c<2011,才能使两个图象有三个公共点,最后综合以上两点,可得出a+b+c的取值范围.
解答:作出函数的图象如图,直线y=y交函数图象于如图,由正弦曲线的对称性,
可得A(a,y)与B(b,y)关于直线x= 对称,因此a+b=1
对称,因此a+b=1
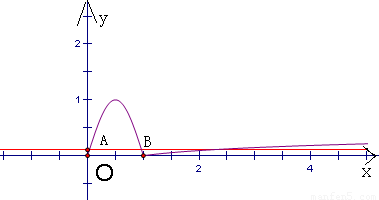
当直线线y=y向上平移时,经过点(2011,1)时图象两个图象恰有两个公共点(A、B重合)
所以0<y<1时,两个图象有三个公共点,此时满足f(a)=f(b)=f(c),(a、b、c互不相等),
说明1<c<2011,因此可得a+b+c∈(2,2012)
故答案为(2,2012)
点评:本题以三角函数和对数函数为例,考查了函数的零点与方程根个数讨论等知识点,属于中档题.利用数形结合,观察图象的变化,从而得出变量的取值范围是解决本题的关键.
 对称,故a+b=1,再观察对数函数图象得c满足1<c<2011,才能使两个图象有三个公共点,最后综合以上两点,可得出a+b+c的取值范围.
对称,故a+b=1,再观察对数函数图象得c满足1<c<2011,才能使两个图象有三个公共点,最后综合以上两点,可得出a+b+c的取值范围.解答:作出函数的图象如图,直线y=y交函数图象于如图,由正弦曲线的对称性,
可得A(a,y)与B(b,y)关于直线x=
 对称,因此a+b=1
对称,因此a+b=1
当直线线y=y向上平移时,经过点(2011,1)时图象两个图象恰有两个公共点(A、B重合)
所以0<y<1时,两个图象有三个公共点,此时满足f(a)=f(b)=f(c),(a、b、c互不相等),
说明1<c<2011,因此可得a+b+c∈(2,2012)
故答案为(2,2012)
点评:本题以三角函数和对数函数为例,考查了函数的零点与方程根个数讨论等知识点,属于中档题.利用数形结合,观察图象的变化,从而得出变量的取值范围是解决本题的关键.

练习册系列答案
相关题目
 若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 . 若满足地f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 .
若满足地f(a)=f(b)=f(c),(a、b、c互不相等),则a+b+c的取值范围是 . ,
, ,动点P(x,y)同时满足
,动点P(x,y)同时满足 则z=x+y的最大值是 .
则z=x+y的最大值是 .