题目内容
(理)已知函数g(x)=1-cos(
x+2ψ)(0<ψ<
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
| π |
| 2 |
| π |
| 2 |
分析:先由g(x)过点(1,2),求得φ,进而求得函数g(x),再由g(x)=M 在两个周期之内有四个解,则在在一个周期内必有两个解,表示出四个解来相加可得.
解答:解:因为:函数g(x)=1-cos(
x+2ψ)(0<ψ<
)的图象过点(1,2),
∴1-cos(
+2φ)=2,
∴sin2φ=1,
∴φ=
∴g(x)=1-cos(
x-
)=1-sin
x.
∵g(x)=M 在两个周期之内竟然有四个解,
∴sin
x=1-M在一个周期内有两个解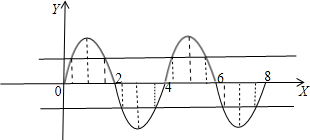
当1-M>0时,四个根中其中两个关于x=11对称,另两个关于x=5对称,故其和为2×1+5×2=12.
当1-M<0时,四个根中其中两个关于x=3对称,另两个关于x=7对称,故其和为2×3+7×2=20.
综上得:x1+x2+x3+x4=12或20.
故选C.
| π |
| 2 |
| π |
| 2 |
∴1-cos(
| π |
| 2 |
∴sin2φ=1,
∴φ=
| π |
| 4 |
∴g(x)=1-cos(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∵g(x)=M 在两个周期之内竟然有四个解,
∴sin
| π |
| 2 |

当1-M>0时,四个根中其中两个关于x=11对称,另两个关于x=5对称,故其和为2×1+5×2=12.
当1-M<0时,四个根中其中两个关于x=3对称,另两个关于x=7对称,故其和为2×3+7×2=20.
综上得:x1+x2+x3+x4=12或20.
故选C.
点评:本题主要考查三角函数的周期性及三角方程有多解的特性,但都有相应的规律,与周期有关.

练习册系列答案
相关题目
 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<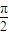 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<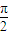 )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )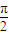 x+2ψ)(0<ψ<
x+2ψ)(0<ψ<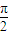 )的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )
)的图象过点(1,2),若有4个不同的正数xi 满足g(xi)=M,且xi<8(i=1,2,3,4),则x1+x2+x3+x4等于( )