Question

（理）已知函数f(x)=

sinπx x∈[0，1] log2011x x∈(1，+∞)

若满足地f（a）=f（b）=f（c），（a、b、c互不相等），则a+b+c的取值范围是

 

．
（文）在平面直角坐标系xOy中，设

OM

=(1，

1

2

)，

ON

=(0，1)，动点P（x，y）同时满足

0≤ OP • OM ≤1 0≤ OP • ON ≤1

则z=x+y的最大值是

 

．

Answer 1

分析：（理）画出函数f（x）=f(x)=

sinπx x∈[0，1] log2011x x∈(1，+∞)

的图象，根据f（a）=f（b）=f（c），不妨a＜b＜c，结合图象求出a+b+c的范围即可．
（文）利用向量的数量积求出x，y的约束条件，画出可行域，将目标函数变形得到z的几何意义，画出目标函数对应的直线，数形结合求出最值．

解答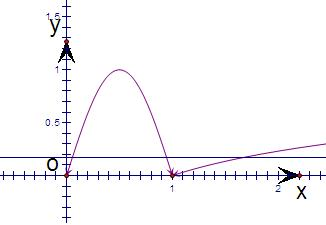：解：（理）作出函数f（x）的图象如图，
不妨设a＜b＜c，则a+b=1，c∈（1，2011）
a+b+c=1+c∈（2，2012）
故答案为：（2，2012）．
（文）：

OP

•

OM

=x+

1

2

y，

OP

•

ON

=y
据题意得

0≤x+ 1 2 y≤1 0≤y≤1

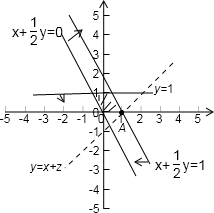画出可行域
将z=x+y变形为y=-x+z画出相应的直线，将直线平移至可行域中的点（

1

2

，1）时，纵截距最大，z最大将（

1

2

，1）代入z=x+y得到z的最大值

3

2

故答案为

3

2

点评：（1）本小题主要考查分段函数、对数的运算性质以及利用数形结合解决问题的能力．解答的关键是图象法的应用，即利用函数的图象交点研究方程的根的问题．
（2）本题考查向量的数量积公式、画出不等式组的可行域、给目标函数赋予几何意义、数形结合求最值．