Question

【题目】已知顶点在原点，焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ．
（1）求抛物线的方程；
（2）若抛物线与直线y=2x﹣5无公共点，试在抛物线上求一点，使这点到直线y=2x﹣5的距离最短．

Answer 1

【答案】
（1）解：设抛物线的方程为y2=2px，则 ，

消去y得

= ，

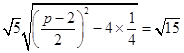则 ，p2﹣4p﹣12=0，

∴p=﹣2，或p=6，

∴y2=﹣4x，或y2=12x

（2）解：解法一、显然抛物线y2=﹣4x与直线y=2x﹣5无公共点，

设点 为抛物线y2=﹣4x上的任意一点，

点P到直线y=2x﹣5的距离为d，

则

当t=﹣1时，d取得最小值，

此时 为所求的点

解法二、显然抛物线y2=﹣4x与直线y=2x﹣5无公共点，

设与直线y=2x﹣5平行且与抛物线y2=﹣4x相切的直线方程为y=2x+b，

切点为P，则点P即为所求点．

由 ，

消去y并化简得：4x2+4（b+1）x+b2=0，

∵直线与抛物线相切，

∴△=16（b+1）2﹣16b2=0，

解得：

把 代入方程4x2+4（b+1）x+b2=0并解得： ，∴y=﹣1

故所求点为

【解析】（1）设抛物线的方程为y2=2px，由 ，得 ，由抛物线被直线y=2x+1截得的弦长为 能求出抛物线方程．（2）法一、抛物线y2=﹣4x与直线y=2x﹣5无公共点，设点 为抛物线y2=﹣4x上的任意一点，点P到直线y=2x﹣5的距离为d，则 ，故当t=﹣1时，d取得最小值． 法二、抛物线y2=﹣4x与直线y=2x﹣5无公共点，设与直线y=2x﹣5平行且与抛物线y2=﹣4x相切的直线方程为y=2x+b，
切点为P，则点P即为所求点，由此能求出结果．