题目内容
(12分)已知定义在区间(-1,1)上的函数f(x)既是奇函数又是减函数,G(x)=f(1-x)+f(1-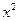 ),
),
求G(x)<0的解
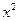 ),
),求G(x)<0的解
略
解:(1)若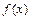 为偶函数,则
为偶函数,则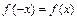 ,即
,即
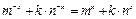 恒成立
恒成立
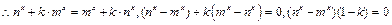
由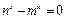 不恒成立,得
不恒成立,得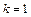
若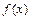 为奇函数,则
为奇函数,则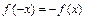 ,即
,即
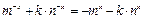 恒成立
恒成立
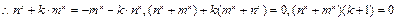
由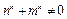 恒成立,得
恒成立,得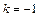
(2)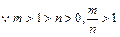
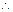 当
当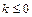 时,显然
时,显然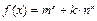 在
在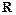 上为增函数;
上为增函数;
当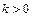 时,
时,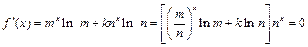
由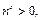 得
得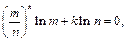 即
即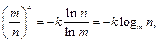
得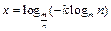
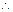 当
当 时,
时,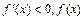 为减函数;
为减函数;
当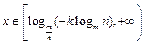 时,
时,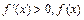 为增函数
为增函数
(3)当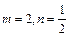 时,
时,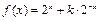 ,
,
若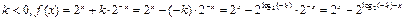 ,
,
则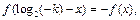
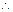 函数
函数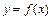 有对称中心
有对称中心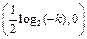
若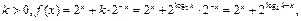 则
则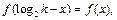
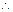 函数
函数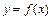 有对称轴
有对称轴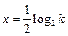
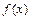 为偶函数,则
为偶函数,则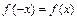 ,即
,即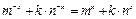 恒成立
恒成立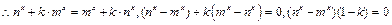
由
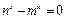 不恒成立,得
不恒成立,得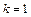
若
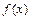 为奇函数,则
为奇函数,则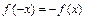 ,即
,即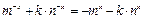 恒成立
恒成立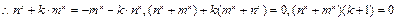
由
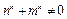 恒成立,得
恒成立,得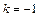
(2)
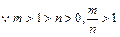
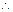 当
当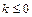 时,显然
时,显然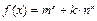 在
在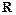 上为增函数;
上为增函数;当
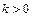 时,
时,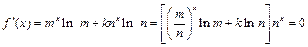
由
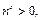 得
得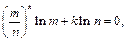 即
即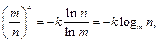
得
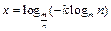
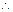 当
当 时,
时,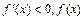 为减函数;
为减函数;当
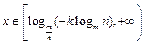 时,
时,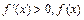 为增函数
为增函数(3)当
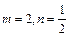 时,
时,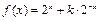 ,
,若
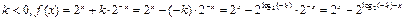 ,
,则
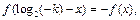
 函数
函数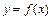 有对称中心
有对称中心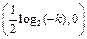
若
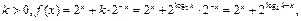 则
则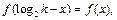
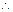 函数
函数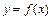 有对称轴
有对称轴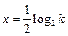

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
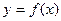 的定义域为R,对任意
的定义域为R,对任意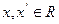 ,均有
,均有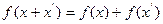 ,且对任意
,且对任意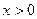 都有
都有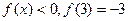 。
。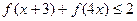 。
。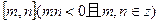 上的值域;
上的值域;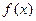 为定义在
为定义在 上的奇函数,当
上的奇函数,当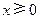 时,
时,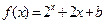 (
(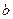 为常数),则
为常数),则 ( )
( )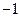
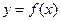 与
与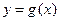 有相同的定义域,且都不是常值函数,对于定义域
有相同的定义域,且都不是常值函数,对于定义域 内的任何
内的任何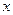 , 有
, 有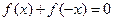 ,
, ,且当
,且当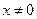 时,
时, ,则
,则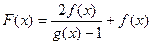 的奇偶性为 ( )
的奇偶性为 ( )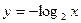
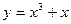
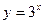
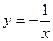
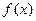 为定义在
为定义在 上的奇函数,当
上的奇函数,当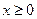 时,
时,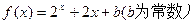 ,则
,则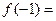 ( )
( )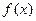 是定义在区间
是定义在区间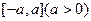 上的奇函数,
上的奇函数,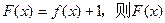 的最大值与最小值之和为
的最大值与最小值之和为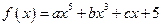 ,若
,若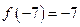 ,则
,则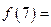
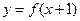 为R上的偶函数,
为R上的偶函数,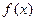 的导函数为
的导函数为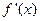 且
且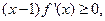
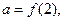
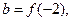
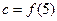 ,则实数a,b,c的大小为 。
,则实数a,b,c的大小为 。