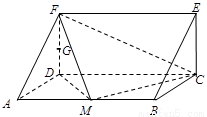题目内容
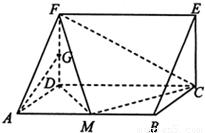
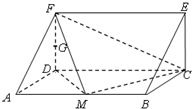 如图,在三棱柱ADF-BCE中,侧棱AB⊥底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,M、G分别是AB、DF的中点.
如图,在三棱柱ADF-BCE中,侧棱AB⊥底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,M、G分别是AB、DF的中点.(1)求证GA∥平面FMC;
(2)求直线DM与平面ABEF所成角.
分析:(1)欲证GA∥平面FMC,可先证明面GSA∥面FMC,取DC中点S,连接AS、GS、GA,根据中位线定理可知GS∥FC,AS∥CM,满足面面平行的判定定理,而GA?面GSA,满足面面平行的性质,从而得到结论;
(2)在平面ADF上,过D作AF的垂线,垂足为H,连DM,则DH⊥平面ABEF,根据线面所成角的定义可知∠DMH是DM与平面ABEF所成的角.在RT△DHM中,求出此角即可.
(2)在平面ADF上,过D作AF的垂线,垂足为H,连DM,则DH⊥平面ABEF,根据线面所成角的定义可知∠DMH是DM与平面ABEF所成的角.在RT△DHM中,求出此角即可.
解答: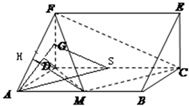 解:(1)证明:取DC中点S,连接AS、GS、GA,
解:(1)证明:取DC中点S,连接AS、GS、GA,
∵G是DF的中点,GS∥FC,AS∥CM
∴面GSA∥面FMC,而GA?面GSA,
∴GA∥平面FMC
(2)在平面ADF上,过D作AF的垂线,垂足为H,连DM,则DH⊥平面ABEF,
∠DMH是DM与平面ABEF所成的角.
在RT△DHM中,DH=
a,DM=
a
∴sin∠DMH=
=
,
∠DMH=
所以DM与平面ABEF所成的角为
.
 解:(1)证明:取DC中点S,连接AS、GS、GA,
解:(1)证明:取DC中点S,连接AS、GS、GA,∵G是DF的中点,GS∥FC,AS∥CM
∴面GSA∥面FMC,而GA?面GSA,
∴GA∥平面FMC
(2)在平面ADF上,过D作AF的垂线,垂足为H,连DM,则DH⊥平面ABEF,
∠DMH是DM与平面ABEF所成的角.
在RT△DHM中,DH=
| ||
| 2 |
| 2 |
∴sin∠DMH=
| DH |
| DM |
| 1 |
| 2 |
∠DMH=
| π |
| 6 |
所以DM与平面ABEF所成的角为
| π |
| 6 |
点评:本题主要考查了直线与平面的所成角,以及直线与平面平行的判定,同时考查了空间想象能力、计算与推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
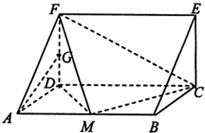 (2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.
(2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.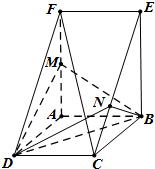 如图,在三棱柱ADF-BCE中,矩形ABCD和矩形ABEF所在的平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE.
如图,在三棱柱ADF-BCE中,矩形ABCD和矩形ABEF所在的平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE.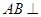 底面
底面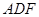 ,底面
,底面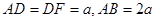 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点.