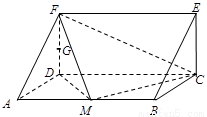题目内容
如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.(I)若M是线段AB的中点,求证:GA∥平面FMC
(II)若多面体BCDMFE的体积是多面体F-ADM的体积的3倍,AM=λMB,求λ的值.
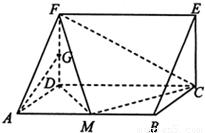
【答案】分析:(I)方法一(面面平行性质法):取DC中点S,连接AS,GS,GA,由三角形中位定理可得GS∥FC,AS∥CM,进而由面面平行的第二判定定理可得面GSA∥面FMC,最后由面面平行的性质,得到答案.
方法二:(线面平行的判定定理法):取FC中点N,连接GN,MN,由三角形中位线定理及平行四边形判定定理,可得AMNG是平行四边形,进而AG∥MN,最后由线面平行的判定定理得到答案.
(II)设三棱柱ADF-BCE的体积为V,多面体F-ADM与多面体DMFEBC的体积分别是V1,V2,AM=x,由多面体BCDMFE的体积是多面体F-ADM的体积的3倍,可求出x与a的关系,进而得到λ值.
解答: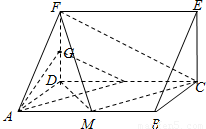 证明:(I)
证明:(I)
方法一(面面平行性质法):
取DC中点S,连接AS,GS,GA
∵G是DF的中点,GS∥FC,AS∥CM
∵GS∩AS=S,GS,AS?面GSA,FC,CM?面FMC
∴面GSA∥面FMC,
而GA?平面GSA,
∴GA∥平面FMC…(6分)
方法二:(线面平行的判定定理法)
取FC中点N,连接GN,MN
∵G是DF中点
∴GF∥CD且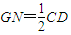
又∵AM∥CD且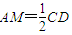
∴AM∥GN且AM=GN
∴AMNG是平行四边形
∴AG∥MN又
∵MN?平面FCM,AG?平面FMC
∴AG∥平面FMC…(6分)
(II)设三棱柱ADF-BCE的体积为V,多面体F-ADM与多面体DMFEBC的体积分别是V1,V2,AM=x.
由题意得, ,
,
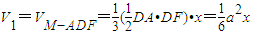 ,
,
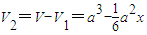 .…(9分)
.…(9分)
因为V2=3V1
所以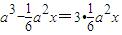 ,解得
,解得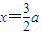 .
.
所以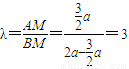 .…(12分)
.…(12分)
点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,其中(I)的关键是熟练线面平行的证明方法和步骤,(II)的关键是由多面体BCDMFE的体积是多面体F-ADM的体积的3倍,求出x与a的关系.
方法二:(线面平行的判定定理法):取FC中点N,连接GN,MN,由三角形中位线定理及平行四边形判定定理,可得AMNG是平行四边形,进而AG∥MN,最后由线面平行的判定定理得到答案.
(II)设三棱柱ADF-BCE的体积为V,多面体F-ADM与多面体DMFEBC的体积分别是V1,V2,AM=x,由多面体BCDMFE的体积是多面体F-ADM的体积的3倍,可求出x与a的关系,进而得到λ值.
解答:
 证明:(I)
证明:(I)方法一(面面平行性质法):
取DC中点S,连接AS,GS,GA
∵G是DF的中点,GS∥FC,AS∥CM
∵GS∩AS=S,GS,AS?面GSA,FC,CM?面FMC
∴面GSA∥面FMC,
而GA?平面GSA,
∴GA∥平面FMC…(6分)
方法二:(线面平行的判定定理法)
取FC中点N,连接GN,MN
∵G是DF中点
∴GF∥CD且
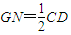
又∵AM∥CD且
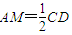
∴AM∥GN且AM=GN
∴AMNG是平行四边形
∴AG∥MN又
∵MN?平面FCM,AG?平面FMC
∴AG∥平面FMC…(6分)
(II)设三棱柱ADF-BCE的体积为V,多面体F-ADM与多面体DMFEBC的体积分别是V1,V2,AM=x.
由题意得,
 ,
,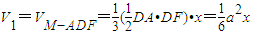 ,
,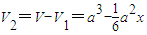 .…(9分)
.…(9分)因为V2=3V1
所以
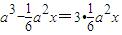 ,解得
,解得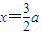 .
.所以
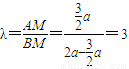 .…(12分)
.…(12分)点评:本题考查的知识点是直线与平面平行的判定,棱锥的体积,其中(I)的关键是熟练线面平行的证明方法和步骤,(II)的关键是由多面体BCDMFE的体积是多面体F-ADM的体积的3倍,求出x与a的关系.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
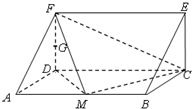 如图,在三棱柱ADF-BCE中,侧棱AB⊥底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,M、G分别是AB、DF的中点.
如图,在三棱柱ADF-BCE中,侧棱AB⊥底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,M、G分别是AB、DF的中点.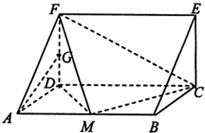 (2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.
(2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.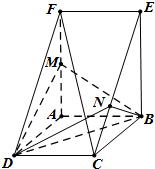 如图,在三棱柱ADF-BCE中,矩形ABCD和矩形ABEF所在的平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE.
如图,在三棱柱ADF-BCE中,矩形ABCD和矩形ABEF所在的平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE.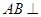 底面
底面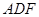 ,底面
,底面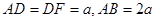 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点.