题目内容
证明：过抛物线y=a（x-x1）•（x-x2）（a≠0，x1＜x2）上两点A（x1，0）、B（x2，0）的切线，与x轴所成的锐角相等．分析：本题考查的主要知识点是导数，由过A（x1，0）、B（x2，0）两点的切线，与x轴所成的锐角相等，我们可得到两条直线的倾斜角相等或互补，则它们的斜率的绝对值应该相等，故利用与x轴所成的锐角和倾斜角之间的关系，只要求出切线的斜率进行比较即可．
解答：解：y′=2ax-a（x1+x2），
y′|_x=x1=a（x1-x2），即kA=a（x1-x2），
y′|_x=x2=a（x2-x1），即kB=a（x2-x1）．
设两条切线与x轴所成的锐角为α、β，
则tanα=|kA|=|a（x1-x2）|，
tanβ=|kB|=|a（x2-x1）|，
故tanα=tanβ．
又α、β是锐角，则α=β．
y′|_x=x1=a（x1-x2），即kA=a（x1-x2），
y′|_x=x2=a（x2-x1），即kB=a（x2-x1）．
设两条切线与x轴所成的锐角为α、β，
则tanα=|kA|=|a（x1-x2）|，
tanβ=|kB|=|a（x2-x1）|，
故tanα=tanβ．
又α、β是锐角，则α=β．
点评：在解题过程中，由tanα=tanβ不能直接得α=β，还必须有α、β为锐角时（或在同一单调区间上时）才能得α=β．
练习册系列答案
相关题目
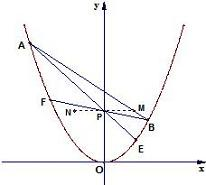已知抛物线y=x2和三个点M（x0，y0）、P（0，y0）、N（-x0，y0）（y0≠x02，y0＞0），过点M的一条直线交抛物线于A、B两点，AP、BP的延长线分别交曲线C于E、F．