题目内容
证明：过抛物线y=a(x－x1)(x－x2)(a≠0, x1< x2)上两点A(x1,0),B(x2,0)的切线与x轴所成的锐角相等。12分
证明见解析
解析:
证明：∵y= a(x－x1)(x－x2)=ax2－a(x1+ x2)x+a x1 x2.…………..3分
∴
=2ax－a(x1+x2) .………….6分
∴k1=│x=x1=a(x1－x2) k2=│x=x2=a(x2－x1) .…………..9分
设两切线与x轴所成锐角为θ1和θ2
则tanθ1=│a(x1－x2)│=│a│(x2－x1)>0, tanθ2=│a(x2－x1)│=│a│(x2－x1)>0………11分
∴tanθ1= tanθ2.…………..12分
练习册系列答案
相关题目
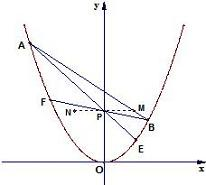已知抛物线y=x2和三个点M（x0，y0）、P（0，y0）、N（-x0，y0）（y0≠x02，y0＞0），过点M的一条直线交抛物线于A、B两点，AP、BP的延长线分别交曲线C于E、F．