题目内容
函数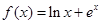 的零点所在的区间是
的零点所在的区间是
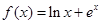 的零点所在的区间是
的零点所在的区间是A.(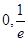 ) ) | B.(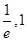 ) ) | C.(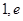 ) ) | D.(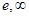 ) ) |
A
由于函数在(0,+∞)单调递增且连续,根据零点判定定理只要满足f(a)f(b)<0即为满足条件的区间
解:由于函数在(0,+∞)单调递增且连续
f(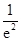 )=e
)=e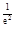 -2<0,f(
-2<0,f(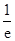 )=ln
)=ln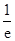 +e
+e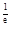 =e
=e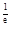 -1>0,f(1)=e>0
-1>0,f(1)=e>0
故满足条件的区间为(0,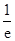 )
)
故选A.
解:由于函数在(0,+∞)单调递增且连续
f(
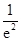 )=e
)=e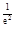 -2<0,f(
-2<0,f(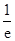 )=ln
)=ln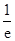 +e
+e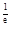 =e
=e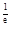 -1>0,f(1)=e>0
-1>0,f(1)=e>0故满足条件的区间为(0,
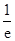 )
)故选A.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
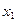 与
与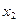 分别是实系数一元二次方程
分别是实系数一元二次方程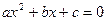 和
和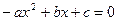 的一个实根,且
的一个实根,且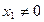 ,
,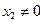 .求证:方程
.求证:方程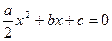 必有一根介于
必有一根介于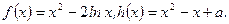
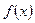 的极值;
的极值;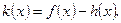 若函数
若函数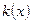 在
在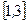 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 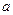 的取值范围.
的取值范围.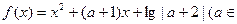
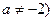
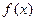 能表示成一个奇函数
能表示成一个奇函数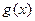 和一个偶函数
和一个偶函数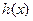 的和,求
的和,求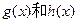 的解析式;
的解析式;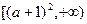 上是增函数与命题Q:.函数
上是增函数与命题Q:.函数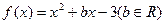 的零点个数是( )
的零点个数是( )


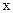 的方程
的方程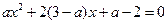 中的
中的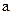 为负整数,则使方程至少有一个整数解时
为负整数,则使方程至少有一个整数解时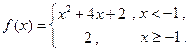 则
则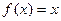 有三个根;
有三个根;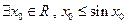 ;
;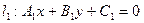 与直线
与直线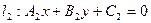 平行的充要条件是
平行的充要条件是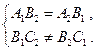
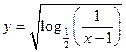 的定义域是
的定义域是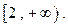
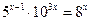 的解集是( ).
的解集是( ).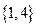 B.
B.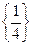 C.
C.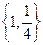 D
D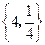
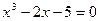 在区间
在区间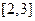 内的实根,取区间中点为
内的实根,取区间中点为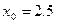 ,那么下一个有根的区间是 .
,那么下一个有根的区间是 . 