Question

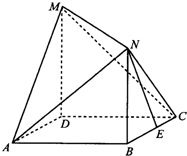如图，四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD=NB=1，E为BC的中点．
（Ⅰ）求异面直线NE与AM所成角的余弦值；
（Ⅱ）在线段AN上是否存在点S，使得ES⊥平面AMN？若存在，求线段AS的长；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）如图，建立空间直角坐标D-xyz，求出两条异面直线上的两个向量的坐标，求出这两个向量
 所成的角的余弦值，再取绝对值，即得异面直线NE与AM所成角的余弦值．
（Ⅱ）假设在线段AN上存在点S，使得ES⊥平面AMN．设

AS

=?λ

AN

，则 

ES

=

EA

+

AS

．
由ES⊥平面AMN，得

ES • AM =0 ES • AN =0

，求得 λ=

1

2

，|AS|=

2

2

．

解答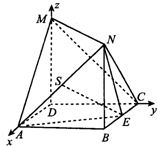：解：（Ⅰ）如图，以D为坐标原点，建立空间直角坐标D-xyz，
依题意，得D（0，0，0），A（1，0，0），M（0，0，1），C（0，1，0），
B（1，1，0），N(1， 1， 1)，E(

1

2

， 1， 0)．
∴

NE

=(-

1

2

，0， -1)，

AM

=(-1， 0， 1)，
∵cos＜

NE

，

AM

＞=

NE • AM

| NE |×| AM |

=-

10

10

，
所以，异面直线NE与AM所成角的余弦值为

10

10

•
（Ⅱ）假设在线段AN上存在点S，使得ES⊥平面AMN．
∵

AN

=（0，1，1），设

AS

=?λ

AN

=（0，λ，λ），

EA

=(

1

2

， -1， 0)，
∴

ES

=

EA

+

AS

=(

1

2

， λ-1， λ)．
由ES⊥平面AMN，得

ES • AM =0 ES • AN =0

，即

- 1 2 +λ=0 (λ-1)+λ=0.

，λ=

1

2

，
此时

AS

=(0，

1

2

，

1

2

)，|

AS

|=

2

2

•  经检验，当|AS|=

2

2

时，ES⊥平面AMN．
故线段AN上存在点S，使得ES⊥平面AMN，此时|AS|=

2

2

．

点评：本题考查异面直线所成的角的定义和求法，证明线面垂直的方法，求平面的法向量的坐标是解题的关键．