题目内容
(2013•东城区一模)已知向量
,
,O是坐标原点,若|
|=k|
|,且
方向是沿
的方向绕着A点按逆时针方向旋转θ角得到的,则称
经过一次(θ,k)变换得到
.现有向量
=(1,1)经过一次(θ1,k1)变换后得到
,
经过一次(θ2,k2)变换后得到
,…,如此下去,
经过一次(θn,kn)变换后得到
.设
=(x,y),θn=
,kn=
,则y-x等于( )
| OA |
| AB |
| AB |
| OA |
| AB |
| OA |
| OA |
| AB |
| OA |
| AA1 |
| AA1 |
| A1A2 |
| An-2An-1 |
| An-1An |
| An-1An |
| 1 |
| 2n-1 |
| 1 |
| cosθn |
分析:根据题意,可得(θ1,k1)=(1,
),即当n=1时,一次(θ1,k1)变换将
逆时针旋转1弧度,再将所得向量的长度再伸长为原来的
倍得到向量
.因此当
=(1,1)时,运用矩阵变换公式,算出
逆时针旋转1弧度所得向量
=(cos1-sin1,sin1+cos1),从而得到
=(x,y)=(1-
,
+1),所以y-x=
.接下来再对A、B、C、D各项在n=1时的情况进行计算,对照所得结果可得只有B项是正确的选项.
| 1 |
| cos1 |
| OA |
| 1 |
| cosθ1 |
| AA1 |
| OA |
| OA |
| a |
| AA1 |
| sin1 |
| cos1 |
| sin1 |
| cos1 |
| 2sin1 |
| cos1 |
解答:解:根据题意,θ1=
=1,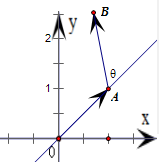 k1=
k1=
=
∴一次(θ1,k1)变换就是将向量
逆时针旋转1弧度,
再将长度伸长为原来的
倍,
即
由
逆时针旋转1弧度而得,且|
|=
|
|
设向量
逆时针旋转1弧度,所得的向量为
=(x',y')
则有
•
=
,
∴
,即向量
逆时针旋转1弧度,
得到向量
=(cos1-sin1,sin1+cos1),再将
的模长度伸长为原来的
倍,
得到
=
(cos1-sin1,sin1+cos1)=(1-
,
+1)
因此当n=1时,
=(x,y)=(1-
,
+1)
即
,由此可得y-x=
+1-(1-
)=
对于A,当n=1时
=
=
=2,与计算结果不相等,故A不正确;
对于B,当n=1时
=
=
,与计算结果相等,故B正确;
对于C,当n=1时
=
=
,与计算结果不相等,故C不正确;
对于D,当n=1时
=
=
=2,与计算结果不相等,故D不正确
综上所述,可得只有B项符合题意
故选:B
| 1 |
| 21-1 |
 k1=
k1=| 1 |
| cosθ1 |
| 1 |
| cos1 |
∴一次(θ1,k1)变换就是将向量
| OA |
再将长度伸长为原来的
| 1 |
| cos1 |
即
| AA1 |
| OA |
| AA1 |
| 1 |
| cos1 |
| OA |
设向量
| OA |
| a |
则有
|
|
|
∴
|
| OA |
得到向量
| a |
| a |
| 1 |
| cos1 |
得到
| AA1 |
| 1 |
| cos1 |
| sin1 |
| cos1 |
| sin1 |
| cos1 |
因此当n=1时,
| AA1 |
| sin1 |
| cos1 |
| sin1 |
| cos1 |
即
|
| sin1 |
| cos1 |
| sin1 |
| cos1 |
| 2sin1 |
| cos1 |
对于A,当n=1时
2sin[2-(
| ||||
sin1sin
|
2sin[2-(
| ||
| sin1 |
| 2sin1 |
| sin1 |
对于B,当n=1时
2sin[2-(
| ||||
cos1cos
|
2cos[2-(
| ||
| cos1 |
| 2sin1 |
| cos1 |
对于C,当n=1时
2cos[2-(
| ||||
sin1sin
|
2cos[2-(
| ||
| sin1 |
| 2cos1 |
| sin1 |
对于D,当n=1时
2cos[2-(
| ||||
cos1cos
|
2cos[2-(
| ||
| cos1 |
| 2cos1 |
| cos1 |
综上所述,可得只有B项符合题意
故选:B
点评:本题给出向量的旋转和伸缩,求向量
=(1,1)经过n变换(θn,kn)后得到的向量坐标,着重考查了向量的线性运算、用矩阵解决向量旋转问题和数列的通项公式等知识,属于中档题.
| OA |

练习册系列答案
相关题目
 (2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若
(2013•东城区一模)数列{an}的各项排成如图所示的三角形形状,其中每一行比上一行增加两项,若