题目内容
给定四条曲线:①x2+y2=
,②
+
=1,③x2+
=1,④
+y2=1,其中与直线x+y-
=0仅有一个交点的曲线是( )
| 5 |
| 2 |
| x2 |
| 9 |
| y2 |
| 4 |
| y2 |
| 4 |
| x2 |
| 4 |
| 5 |
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
分析:判断直线和圆的位置关系时,只要比较圆心到这条直线的距离d与半径r的大小即可.当d<r时,直线和圆相交,有两个交点;当d=r时,直线和圆相切,有一个交点;当d>r时,直线和圆想离,无交点;判断直线和椭圆的交点个数时,联立直线方程和椭圆方程,整理,由△的符号即可判断出其交点个数.当△>0时,有两个交点;当△=0时,有一个交点;当△<0时,无交点,据此计算可得答案.
解答:解:①中,圆心(0,0)到直线x+y-
=0的距离为
等于半径,故满足题意.
②中,联立方程
,整理得,13x2-18
x+9=0.△≠0,故不满足题意.
③中,联立方程
.整理得,5x2-2
x+1=0.△=0,故满足题意.
④中,联立方程
,整理得,5x2-8
x+16=0,△=0.故满足题意.
故本题中①③④满足,答案为D.
| 5 |
| ||
|
②中,联立方程
|
| 5 |
③中,联立方程
|
| 5 |
④中,联立方程
|
| 5 |
故本题中①③④满足,答案为D.
点评:在判定直线和圆锥曲线的交点个数时,可联立方程组,由方程组的解的个数从而确定交点的个数.对于判断圆和直线的位置关系时,除此之外,还可以用更为简单的几何方法,用圆心到直线的距离与半径作比较.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
给定四条曲线:①x2+y2=
,②
+
=1,③x2+
=1,④,其中与直线x+y-
=0仅有一个交点的曲线是( )
| 5 |
| 2 |
| x2 |
| 9 |
| y2 |
| 4 |
| y2 |
| 4 |
| 5 |
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
 ,②
,②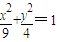 ,③x2+
,③x2+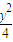 =1,④,其中与直线x+y-
=1,④,其中与直线x+y-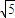 =0仅有一个交点的曲线是( )
=0仅有一个交点的曲线是( )