题目内容
已知函数f(x)=ax2+4x-2,若对任意x1,x2∈R且x1≠x2,都有 .
.
(1)求实数a的取值范围;
(2)对于给定的实数a,有一个最小的负数M(a),使得x∈[M(a),0]时,-4≤f(x)≤4都成立,则当a为何值时,M(a)最小,并求出M(a)的最小值.
解:(1)∵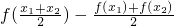
=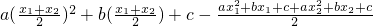
=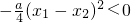 ,
,
∵x1≠x2,∴a>0.∴实数a的取值范围为(0,+∞).
(2)∵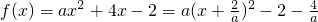 ,
,
显然f(0)=-2,对称轴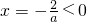 .
.
①当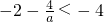 ,即0<a<2时,
,即0<a<2时,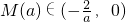 ,且f[M(a)]=-4.
,且f[M(a)]=-4.
令ax2+4x-2=-4,解得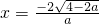 ,
,
此时M(a)取较大的根,即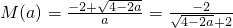 ,
,
∵0<a<2,∴ .
.
②当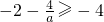 ,即a≥2时,
,即a≥2时,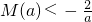 ,且f[M(a)]=4.
,且f[M(a)]=4.
令ax2+4x-2=4,解得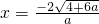 ,
,
此时M(a)取较小的根,即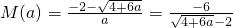 ,
,
∵a≥2,∴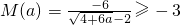 .当且仅当a=2时,取等号.
.当且仅当a=2时,取等号.
∵-3<-1∴当a=2时,M(a)取得最小值-3.
分析:(1)先将 用函数f(x)的表达式表示出来,再进行化简得:
用函数f(x)的表达式表示出来,再进行化简得: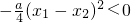 ,由此式即可求得实数a的取值范围;
,由此式即可求得实数a的取值范围;
(2)本小题可以从a的范围入手,考虑0<a<2与a≥2两种情况,结合二次的象与性质,综合运用分类讨论思想与数形结合思想求解.
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
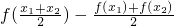
=
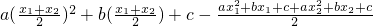
=
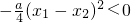 ,
,∵x1≠x2,∴a>0.∴实数a的取值范围为(0,+∞).
(2)∵
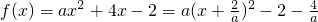 ,
,显然f(0)=-2,对称轴
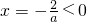 .
.①当
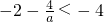 ,即0<a<2时,
,即0<a<2时,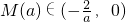 ,且f[M(a)]=-4.
,且f[M(a)]=-4.令ax2+4x-2=-4,解得
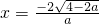 ,
,此时M(a)取较大的根,即
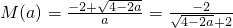 ,
,∵0<a<2,∴
 .
.②当
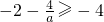 ,即a≥2时,
,即a≥2时,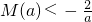 ,且f[M(a)]=4.
,且f[M(a)]=4.令ax2+4x-2=4,解得
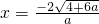 ,
,此时M(a)取较小的根,即
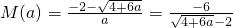 ,
,∵a≥2,∴
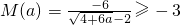 .当且仅当a=2时,取等号.
.当且仅当a=2时,取等号.∵-3<-1∴当a=2时,M(a)取得最小值-3.
分析:(1)先将
 用函数f(x)的表达式表示出来,再进行化简得:
用函数f(x)的表达式表示出来,再进行化简得: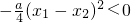 ,由此式即可求得实数a的取值范围;
,由此式即可求得实数a的取值范围;(2)本小题可以从a的范围入手,考虑0<a<2与a≥2两种情况,结合二次的象与性质,综合运用分类讨论思想与数形结合思想求解.
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目