题目内容
设M=10a2+81a+207,P=a+2,Q=26-2a;若将lgM,lgQ,lgP适当排序后可构成公差为1的等差数列{an}的前三项.
(1)试比较M、P、Q的大小;
(2)求a的值及{an}的通项;
(3)记函数f(x)=anx2+2an+1x+an+2(n∈N*)的图象在x轴上截得的线段长为bn,设Tn=
(b1b2+b2b3+…+bn-1bn)(n≥2),求Tn,并证明T2T3T4…Tn>
.
(1)试比较M、P、Q的大小;
(2)求a的值及{an}的通项;
(3)记函数f(x)=anx2+2an+1x+an+2(n∈N*)的图象在x轴上截得的线段长为bn,设Tn=
| 1 |
| 4 |
| 2n-1 |
| n |
分析:(1)由M>0,P>0,Q>0可求得a的范围,作差后通过分类讨论可比较它们间的大小关系;
(2)由(1)的结论及lgM,lgQ,lgP成公差为1的等差数列可得a值,根据等差数列的通项公式可得an;
(3)设f(x)与x轴交点为(x1,0),(x2,0),由2an+1=an+an+2,知-1为f(x)的一个零点,从而f(x)=(x+1)(anx+an+2)=0,可得x1,x2,进而可得bn,利用裂项相消法可得Tn,由Tn=
>
=
,可对T2T3T4…Tn进行放缩得到结论;
(2)由(1)的结论及lgM,lgQ,lgP成公差为1的等差数列可得a值,根据等差数列的通项公式可得an;
(3)设f(x)与x轴交点为(x1,0),(x2,0),由2an+1=an+an+2,知-1为f(x)的一个零点,从而f(x)=(x+1)(anx+an+2)=0,可得x1,x2,进而可得bn,利用裂项相消法可得Tn,由Tn=
| n-1 |
| (1-2lg2)(n-2lg2) |
| n-1 | ||
|
| 2(n-1) |
| n |
解答:解:(1)由
,得-2<a<13,
∵M-Q=10a2+83a+181>0(∵△1<0),M-P=10a2+80a+205>0(∵△2<0),∴M>Q,M>P,
又∵当-2<a<13时,P-Q=-24+3a,
则当-2<a<8时,P<Q,此时P<Q<M,
当a=8时,P=Q,此时P=Q<M,
当8<a<13时,P>Q,此时Q<P<M;
(2)由(1)知,当-2<a<8时,
即
,∴
,
解得a=
,从而an=lgP+(n-1)×1=n-2lg2;
当8<a<13时,
即
,∴
,a无解.
综上,a=
,an=n-2lg2;
(3)设f(x)与x轴交点为(x1,0),(x2,0),
∵2an+1=an+an+2,∴-1为f(x)的一个零点,
∴当f(x)=0时有(x+1)(anx+an+2)=0,∴x1=-1, x2=-
=-
,
∴bn=|x1-x2|=|-1+
|=
,
又∵an=n-2lg2>0,∴bn=
,
∴bn-1bn=
×
=4(
-
),
∴Tn=
×4[(
-
)+(
-
)+…+(
-
)]=
-
=
-
=
,
又Tn=
>
=
,
∴T2T3T4…Tn>
•
•
•
…
=
.
|
∵M-Q=10a2+83a+181>0(∵△1<0),M-P=10a2+80a+205>0(∵△2<0),∴M>Q,M>P,
又∵当-2<a<13时,P-Q=-24+3a,
则当-2<a<8时,P<Q,此时P<Q<M,
当a=8时,P=Q,此时P=Q<M,
当8<a<13时,P>Q,此时Q<P<M;
(2)由(1)知,当-2<a<8时,
|
|
|
解得a=
| 1 |
| 2 |
当8<a<13时,
|
|
|
综上,a=
| 1 |
| 2 |
(3)设f(x)与x轴交点为(x1,0),(x2,0),
∵2an+1=an+an+2,∴-1为f(x)的一个零点,
∴当f(x)=0时有(x+1)(anx+an+2)=0,∴x1=-1, x2=-
| an+2 |
| an |
| an+2 |
| an |
∴bn=|x1-x2|=|-1+
| an+2 |
| an |
| 2 |
| |an| |
又∵an=n-2lg2>0,∴bn=
| 2 |
| an |
∴bn-1bn=
| 2 |
| an-1 |
| 2 |
| an |
| 1 |
| an-1 |
| 1 |
| an |
∴Tn=
| 1 |
| 4 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| an |
| 1 |
| 1-2lg2 |
| 1 |
| n-2lg2 |
| n-1 |
| (1-2lg2)(n-2lg2) |
又Tn=
| n-1 |
| (1-2lg2)(n-2lg2) |
| n-1 | ||
|
| 2(n-1) |
| n |
∴T2T3T4…Tn>
| 2 |
| 2 |
| 2•2 |
| 3 |
| 2•3 |
| 4 |
| 2•4 |
| 5 |
| 2(n-1) |
| n |
| 2n-1 |
| n |
点评:本题考查数列与不等式的综合、等差数列的通项公式,考查不等式的证明,考查学生综合运用知识分析问题解决问题的能力,综合性强,运算量大.

练习册系列答案
相关题目
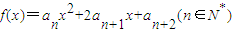 的图象在x轴上截得的线段长为bn,设
的图象在x轴上截得的线段长为bn,设 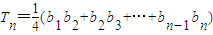 ,求Tn.
,求Tn.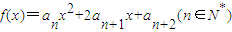 的图象在x轴上截得的线段长为bn,设
的图象在x轴上截得的线段长为bn,设 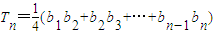 ,求Tn.
,求Tn.