题目内容
设函数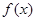 的定义域为
的定义域为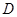 ,若存在非零实数
,若存在非零实数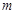 满足
满足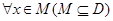 ,均有
,均有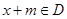 ,且
,且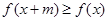 ,则称
,则称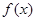 为
为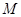 上的
上的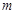 高调函数.如果定义域为
高调函数.如果定义域为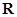 的函数
的函数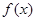 是奇函数,当
是奇函数,当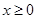 时,
时,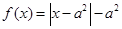 ,且
,且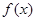 为
为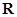 上的
上的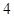 高调函数,那么实数
高调函数,那么实数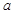 的取值范围是( )
的取值范围是( )
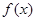 的定义域为
的定义域为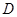 ,若存在非零实数
,若存在非零实数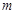 满足
满足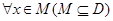 ,均有
,均有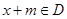 ,且
,且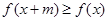 ,则称
,则称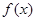 为
为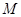 上的
上的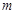 高调函数.如果定义域为
高调函数.如果定义域为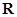 的函数
的函数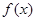 是奇函数,当
是奇函数,当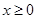 时,
时,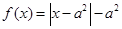 ,且
,且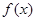 为
为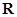 上的
上的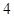 高调函数,那么实数
高调函数,那么实数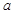 的取值范围是( )
的取值范围是( ) A. | B. | C. | D. |
A
因为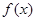 是定义在R上的奇函数,所以当
是定义在R上的奇函数,所以当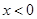 时,
时,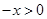 ,则
,则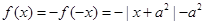 。
。
所以当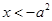 时,
时,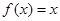 单调递增;当
单调递增;当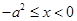 时,
时,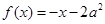 单调递减;当
单调递减;当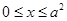 时,
时,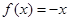 单调递减;当
单调递减;当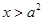 时,
时,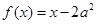 单调递增。
单调递增。
依题意可得,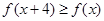 恒成立,所以由单调性可知当
恒成立,所以由单调性可知当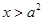 或
或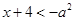 时显然成立,所以当
时显然成立,所以当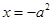 时
时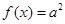 ,此时
,此时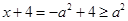 且
且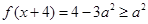 ,所以有
,所以有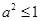 ,解得
,解得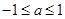 ,故选A
,故选A
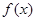 是定义在R上的奇函数,所以当
是定义在R上的奇函数,所以当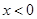 时,
时,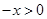 ,则
,则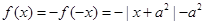 。
。所以当
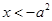 时,
时,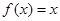 单调递增;当
单调递增;当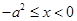 时,
时,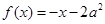 单调递减;当
单调递减;当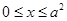 时,
时,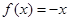 单调递减;当
单调递减;当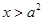 时,
时,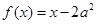 单调递增。
单调递增。依题意可得,
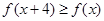 恒成立,所以由单调性可知当
恒成立,所以由单调性可知当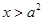 或
或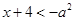 时显然成立,所以当
时显然成立,所以当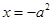 时
时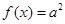 ,此时
,此时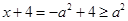 且
且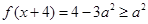 ,所以有
,所以有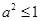 ,解得
,解得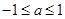 ,故选A
,故选A
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
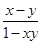 );当x∈(-1,0)时,有f(x)>0.若p=f(
);当x∈(-1,0)时,有f(x)>0.若p=f(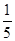 )+f(
)+f(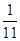 ),Q=f(
),Q=f(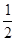 ),R=f(0);则 P,Q,R的大小关系为
),R=f(0);则 P,Q,R的大小关系为 有两个根,其中一个根在区间(—1,0)内,另一个根在区间(1,2)内,求m的取值范围。
有两个根,其中一个根在区间(—1,0)内,另一个根在区间(1,2)内,求m的取值范围。 ,若
,若 且
且 ,则一定有
,则一定有 



 可以产生区间[0,1]上的均匀随机数,若
可以产生区间[0,1]上的均匀随机数,若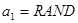 ,
,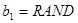 且
且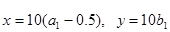 ,
,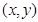 为点
为点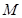 的坐标,则点
的坐标,则点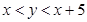 的概率是 .
的概率是 . 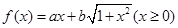 的图像经过(o,1),且
的图像经过(o,1),且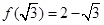
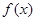 的值域;
的值域;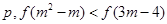 ,命题q:函数
,命题q:函数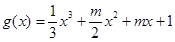 在R上无极值,是否存在实数m满足复合命题p且q为真命题?若存在,求出m的范围;若不存在,说明理由.
在R上无极值,是否存在实数m满足复合命题p且q为真命题?若存在,求出m的范围;若不存在,说明理由.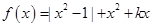
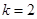 ,求
,求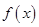 的零点;
的零点;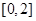 上有两个不同的零点,求
上有两个不同的零点,求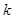 的取值范围。
的取值范围。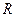 上的函数
上的函数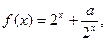
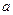 为常数,若
为常数,若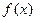 为偶函数
为偶函数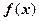 在
在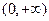 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;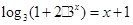 的解
的解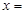 ________。
________。