题目内容
已知点A、B分别是椭圆
+
=1（a＞b＞0）长轴的左、右端点，点C是椭圆短轴的一个端点，且离心率e=
，S△ABC=
．动直线，l：y=kx+m与椭圆于M、N两点．
（I）求椭圆的方程；
（II）若椭圆上存在点P，满足
+
=λ
（O为坐标原点），求λ的取值范围；
（III）在（II）的条件下，当λ取何值时，△MNO的面积最大，并求出这个最大值．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
（I）求椭圆的方程；
（II）若椭圆上存在点P，满足
| OM |
| ON |
| OP |
（III）在（II）的条件下，当λ取何值时，△MNO的面积最大，并求出这个最大值．
（I）由题意，
，∴a=
，b=1
∴椭圆的方程为
+y2=1；
（II）y=kx+m代入椭圆方程整理可得（1+2k2）x2+4kmx+2m2-2=0．
设点M、N的坐标分别为M（x1，y1）、N（x2，y2）、P（x0，y0），则
x1+x2=-
，x1x2=
∴y1+y2=k（x1+x2）+2m=
（1）当m=0时，点M、N关于原点对称，则λ=0．
（2）当m≠0时，点M、N不关于原点对称，则λ≠0，
∵
+
=λ
，∴（x1，y1）+（x2，y2）=λ（x0，y0），
∴x1+x2=λx0，y1+y2=λy0，
∴x0=-
，y0=
∵P在椭圆上，
∴[
]2+2[
]2=2
化简，得4m2（1+2k2）=λ2（1+2k2）2．
∵1+2k2≠0，
∴有4m2=λ2（1+2k2）．…①
又∵△=16k2m2-4（1+2k2）（2m2-2）=8（1+2k2-m2），
∴由△＞0，得1+2k2＞m2．…②
将①、②两式，∵m≠0，∴λ2＜4，
∴-2＜λ＜2且λ≠0．
综合（1）、（2）两种情况，得实数λ的取值范围是-2＜λ＜2；
（III）由题意，|MN|=
|x1-x2|，点O到直线MN的距离d=
∴S△MNO=
|MN|d=
|m||x1-x2|=
由①得1+2k2=
，代入上式并化简可得S△MNO=
•
∵
≤
=2
∴S△MNO≤
当且仅当λ2=4-λ2，即λ=±
时，等号成立
∴当λ=±
时，△MNO的面积最大，最大值为
．
|
| 2 |
∴椭圆的方程为
| x2 |
| 2 |
（II）y=kx+m代入椭圆方程整理可得（1+2k2）x2+4kmx+2m2-2=0．
设点M、N的坐标分别为M（x1，y1）、N（x2，y2）、P（x0，y0），则
x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-2 |
| 1+2k2 |
∴y1+y2=k（x1+x2）+2m=
| 2m |
| 1+2k2 |
（1）当m=0时，点M、N关于原点对称，则λ=0．
（2）当m≠0时，点M、N不关于原点对称，则λ≠0，
∵
| OM |
| ON |
| OP |
∴x1+x2=λx0，y1+y2=λy0，
∴x0=-
| 4km |
| λ(1+2k2) |
| 2m |
| λ(1+2k2) |
∵P在椭圆上，
∴[
| 4km |
| λ(1+2k2) |
| 2m |
| λ(1+2k2) |
化简，得4m2（1+2k2）=λ2（1+2k2）2．
∵1+2k2≠0，
∴有4m2=λ2（1+2k2）．…①
又∵△=16k2m2-4（1+2k2）（2m2-2）=8（1+2k2-m2），
∴由△＞0，得1+2k2＞m2．…②
将①、②两式，∵m≠0，∴λ2＜4，
∴-2＜λ＜2且λ≠0．
综合（1）、（2）两种情况，得实数λ的取值范围是-2＜λ＜2；
（III）由题意，|MN|=
| 1+k2 |
| |m| | ||
|
∴S△MNO=
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 1+2k2 |
由①得1+2k2=
| 4m2 |
| λ2 |
| ||
| 4 |
| λ2(4-λ2) |
∵
| λ2(4-λ2) |
| λ2+(4-λ2) |
| 2 |
∴S△MNO≤
| ||
| 2 |
当且仅当λ2=4-λ2，即λ=±
| 2 |
∴当λ=±
| 2 |
| ||
| 2 |
练习册系列答案
相关题目
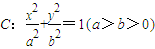过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．
过点
，离心率
，若点M（x，y）在椭圆C上，则点
称为点M的一个“椭点”，直线l交椭圆C于A、B两点，若点A、B的“椭点”分别是P、Q，且以PQ为直径的圆经过坐标原点O．