题目内容

11．二次函数f（x）满足f（x）=x没有实根，则方程f（f（x））=x的实根情况是（　　）
A．有两不等实根B．有两相等实根C．无实根D．都有可能

分析 不妨设b=0，c=1代入到f[f（x）]=x并整理得，x4=-2x2+x-2，可知x4最小值为0，-2x2+x-2最大值-$\frac{15}{8}$，即可得出方程f（f（x））=x的实根情况．

解答 解：设f（x）=ax2+bx+c，则f（x）=x化为ax2+（b-1）x+c=0，
由题意知，判别式△=（b-1）2-4c＜0．
不妨设b=0，c=1代入到f[f（x）]=x并整理得，x4=-2x2+x-2
可知x4最小值为0，-2x2+x-2最大值-$\frac{15}{8}$，
所以f[f（x）]=x无实数根，
故选：C．

点评 本题考查方程根的讨论，考查判别式的运用，比较基础．

练习册系列答案
相关题目
1．已知集合A={x|ax2+2x+1=0}．若A中至少有一个元素，求实数a的取值范围．
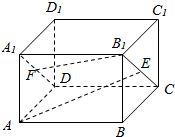2．如图，在长方体ABCD-A1B1C1D1中，E是矩形BCC1B1的中点，F是矩形ADD1A1的中心，连接AE，B1F，判断AE与B1F是否为异面直线．
19．设全集U=R．且A={x|x≤-1或x≥2}．B={y|y＞a}，
（1）若A∪B=A．求实数a的取值范围．
（2）若∁RA⊆B，求实数a的取值范围．
6．指出下列各组中集合A与B之间的关系．
 （1）A={-1，1}，B=Z；
（2）A=N+，B=N；
（3）A={（a，b）}，B={（b，a）}；
（4）A={1，-1}，B={-1，1}；
（5）A={x|x＞3}，B={x|3x-6＞0|；
（6）A=∅，B={x|x2＜-1|；
（7）A={x|x是矩形}，B={x|x是平行四边形}；
（8）A={1，3，5，15}，B={x|x是15的正因数}．
16．已知集合A={1，3，-x3}，B={x+2，1}，是否存在实数x，使得B是A的子集？若存在，求出集合A，B；若不存在，请说明理由．
3．已知函数f（x）=log2（ax2+ax+1）的值域为R，则实数a的取值范围是（　　）
A．（4，+∞）B．（-∞，4）C．[4，+∞）D．（-∞，4]
7．已知两点A（-2，-1），B（-1，2）若直线l过点P（0，-1）且与线段AB有公共点，求直线l的斜率的取值范围．
8．将一段长4m的细线剪为2段，其中一段大于1m，另一段大于2m的概率为$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网