题目内容
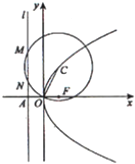 (2013•福建)如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.
(2013•福建)如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|CO|为半径作圆,设圆C与准线l交于不同的两点M,N.(I)若点C的纵坐标为2,求|MN|;
(II)若|AF|2=|AM|•|AN|,求圆C的半径.
分析:(I)由抛物线的方程表示出焦点F的坐标及准线方程,求出C到准线的距离,再利用圆中弦长公式即可求出|MN|的长;
(II)设C(
,y0),表示出圆C的方程方程,与抛物线解析式联立组成方程组,设M(-1,y1),N(-1,y2),利用韦达定理表示出y1y2,利用|AF|2=|AM|•|AN|,得|y1y2|=4,解得C的纵坐标,从而得到圆心C坐标,由两点间的距离公式求出|OC|的长,即为圆的半径.
(II)设C(
| ||
| 4 |
解答:解:(I)抛物线E:y2=4x的准线l:x=-1,
由点C的纵坐标为2,得C(1,2),故C到准线的距离d=2,又|OC|=
,
∴|MN|=2
=2
=2.
(II)设C(
,y0),则圆C的方程为(x-
)2+(y-y0)2=
+
,
即x2-
x+y2-2y0y=0,由x=-1得y2-2y0y+1+
=0,
设M(-1,y1),N(-1,y2),则
,
由|AF|2=|AM|•|AN|,得|y1y2|=4,
∴1+
=4,解得y0=±
,此时△>0
∴圆心C的坐标为(
,±
),|OC|2=
,
从而|OC|=
.
即圆C的半径为
.
由点C的纵坐标为2,得C(1,2),故C到准线的距离d=2,又|OC|=
| 5 |
∴|MN|=2
| |OC|2-d2 |
| 5-4 |
(II)设C(
| ||
| 4 |
| ||
| 4 |
| ||
| 16 |
| y | 2 0 |
即x2-
| ||
| 2 |
| ||
| 2 |
设M(-1,y1),N(-1,y2),则
|
由|AF|2=|AM|•|AN|,得|y1y2|=4,
∴1+
| ||
| 2 |
| 6 |
∴圆心C的坐标为(
| 3 |
| 2 |
| 6 |
| 33 |
| 4 |
从而|OC|=
| ||
| 2 |
即圆C的半径为
| ||
| 2 |
点评:此题考查了圆的标准方程,涉及的知识有:抛物线的简单性质,韦达定理.其中根据题意确定出圆心与半径是解本题的关键.

练习册系列答案
相关题目
 (2013•福建)如图,在△ABC中,已知点D在BC边上,AD⊥AC,
(2013•福建)如图,在△ABC中,已知点D在BC边上,AD⊥AC,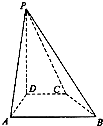 (2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
(2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.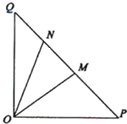 (2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2
(2013•福建)如图,在等腰直角△OPQ中,∠POQ=90°,OP=2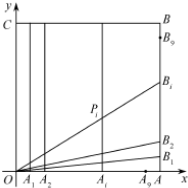 (2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点
(2013•福建)如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点 (2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)