题目内容
已知抛物线C：y2＝4x，F为其焦点，
(1)若过焦点F且斜率为1的直线与抛物线C交于A、B两点，求弦AB的长；
(2)若过点M(2，1)的一条直线交抛物线C于P、Q两点，且PQ被M平分，求这条直线的方程；
(3)设点R、S是抛物线C上原点O以外的两个动点，且OR⊥OS，若作ON⊥RS，垂足为N，求点N的轨迹方程，并说明它表示什么曲线．
答案：
解析：
解析：
|
解：(1)∵点F(1，0)，…………1分 ∴直线AB的方程为y＝x－1，…………2分 将其代入 设A(x1，y1)，B(x2，y2) ∴|AB|＝|AF|＋|BF|＝x1＋1＋x2＋1＝6＋2＝8…………4分 (2)显然直线PQ的斜率存在，设其为k，则PQ的方程为y－1＝k(x－2)，将其代入 则∵ ∴k＝2，而此时方程有根．∴直线方程为y－1＝2(x－2)即2x－y－3＝0……7分 (3)解：(1)设R(x1，y1)，S(x2，y2)，则y12＝2px1，y22＝2px2， ∴y12y22＝4p2x1x2， ∵OR^ OS，∴x1x2＋y1y2＝0，…………8分 由此即可解得：y1y2＝─16 ∵直线AB的斜率k＝ ∴直线AB的方程为y─y1＝ 即y(y1＋y2)─y1y2＝4x，由(1)可得y＝ ∴直线RS过定点M(4，0)．…………9分 又∵RS^ ON，知点N的轨迹是以原点和点(4，0)为直径的圆(除去原点)．立即可求出方程为(x－2)2＋y2＝4(x≠0)…………10分 |
得x2－6x＋1＝0…………3分
，…………6分
＝
＝
，
(x─
)，
(x─4)，
练习册系列答案
相关题目
·
＝0，则k＝
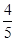B.
C．－