题目内容
已知抛物线C：y2＝4x的焦点为F，过F作C的两条互相垂直的弦AB、CD，设AB、CD的中点分别为M、N．
(Ⅰ)证明直线MN必过定点，并求出这点的坐标；
(Ⅱ)分别以AB、CD为直径作圆，求两圆相交弦的中点H的轨迹方程．
答案：
解析：
解析：
|
解：(Ⅰ)设直线AB： 代入 ∴ 因为 因此直线MN： 故不论 (Ⅱ)因为 两式相减并整理，得公共弦所在直线方程为： 又 故公共弦所在直线过原点 所以，点 其轨迹方程为 |
，
得：
， 2分
，
，故
． 3分
，所以将点
坐标中的
换成
，得
． 4分
，整理得
．
为何值，直线
必过定点
． 6分
、
都与抛物线的准线相切，半径分别为
，从而
，
． 8分
， 9分
，
，所以
．
的轨迹方程是以
为直径的圆(除取直径的两个端点)，
． 12分
练习册系列答案
通城学典默写能手系列答案
相关题目
·
＝0，则k＝
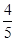B.
C．－