题目内容
已知函数f(x)=x2-ax+a(x∈R),在定义域内有且只有一个零点,存在0<x1<x2,使得不等式f(x1)>f(x2)成立.若n∈N*,f(n)是数列{an}的前n项和.(I)求数列{an}的通项公式;
(II)设各项均不为零的数列{cn}中,所有满足ck•ck+1<0的正整数k的个数称为这个数列{cn}的变号数,令
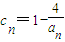 (n为正整数),求数列{cn}的变号数;
(n为正整数),求数列{cn}的变号数;(Ⅲ)设
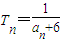 (n≥2且n∈N*),使不等式
(n≥2且n∈N*),使不等式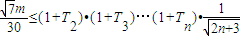 恒成立,求正整数m的最大值.
恒成立,求正整数m的最大值.
【答案】分析:(I)由函数f(x)在定义域内有且只有一个零点,知△=a2-4a=0,得a=0或a=4.由此能求出数列{an}的通项公式.
(II)法一:由题设 ,因为n≥3时,
,因为n≥3时, ,所以n≥3时,数列{cn}递增.由此能够推导出数列{cn}变号数为3.
,所以n≥3时,数列{cn}递增.由此能够推导出数列{cn}变号数为3.
法二:由题设 ,知当n≥2时,令cn•cn+1<0,得
,知当n≥2时,令cn•cn+1<0,得 ,解得n=2或n=4.由此能够推导出数列{cn}变号数为3.
,解得n=2或n=4.由此能够推导出数列{cn}变号数为3.
(Ⅲ)n≥2且n∈N*时,
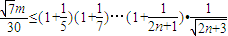 ,转化为
,转化为 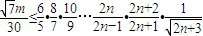 .由此入手能够推导出正整数m的最大值为5.
.由此入手能够推导出正整数m的最大值为5.
解答:解:(I)∵函数f(x)在定义域内有且只有一个零点
∴△=a2-4a=0得a=0或a=4(1分)
当a=0时,函数f(x)=x2在(0,+∞)上递增故不存在0<x1<x2,
使得不等式f(x1)>f(x2)成立 (2分)
综上,得a=4,f(x)=x2-4x+4.(3分)
∴Sn=n2-4n+4
∴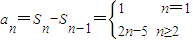 (4分)
(4分)
(II)解法一:由题设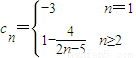
∵n≥3时,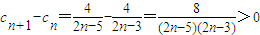
∴n≥3时,数列{cn}递增.
∵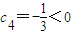 ,
,
由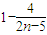 ,得n≥5可知
,得n≥5可知
即n≥3时,有且只有1个变号数;
又即∴此处变号数有2个
综上得数列{cn}共有3个变号数,即变号数为3 (9分)
解法二:由题设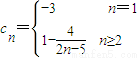
当n≥2时,令cn•cn+1<0,
得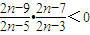 ,
,
即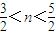 或
或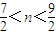 ,
,
解得n=2或n=4.
又∵c1=-3,c2=5,
∴n=1时也有c1•c2<0
综上得数列{cn}共有3个变号数,即变号数为3…(9分)
(Ⅲ)n≥2且n∈N*时,

可转化为 .
.
设g(n)= ,
,
则当n≥2且n∈N*,
=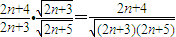
=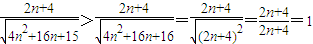 .
.
所以g(n+1)>g(n),即当n增大时,g(n)也增大.
要使不等式
对于任意的n∈N*恒成立,
只需 即可.
即可.
因为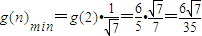 ,
,
所以 .
.
即
所以,正整数m的最大值为5.(13分)
点评:本题考查数列与不等式的综合,计算量大,解题时要认真审题,注意计算能力的培养.本题对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.
(II)法一:由题设
 ,因为n≥3时,
,因为n≥3时, ,所以n≥3时,数列{cn}递增.由此能够推导出数列{cn}变号数为3.
,所以n≥3时,数列{cn}递增.由此能够推导出数列{cn}变号数为3.法二:由题设
 ,知当n≥2时,令cn•cn+1<0,得
,知当n≥2时,令cn•cn+1<0,得 ,解得n=2或n=4.由此能够推导出数列{cn}变号数为3.
,解得n=2或n=4.由此能够推导出数列{cn}变号数为3.(Ⅲ)n≥2且n∈N*时,

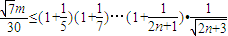 ,转化为
,转化为 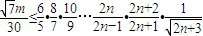 .由此入手能够推导出正整数m的最大值为5.
.由此入手能够推导出正整数m的最大值为5.解答:解:(I)∵函数f(x)在定义域内有且只有一个零点
∴△=a2-4a=0得a=0或a=4(1分)
当a=0时,函数f(x)=x2在(0,+∞)上递增故不存在0<x1<x2,
使得不等式f(x1)>f(x2)成立 (2分)
综上,得a=4,f(x)=x2-4x+4.(3分)
∴Sn=n2-4n+4
∴
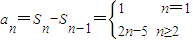 (4分)
(4分)(II)解法一:由题设
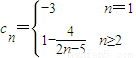
∵n≥3时,
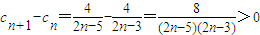
∴n≥3时,数列{cn}递增.
∵
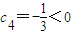 ,
,由
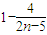 ,得n≥5可知
,得n≥5可知即n≥3时,有且只有1个变号数;
又即∴此处变号数有2个
综上得数列{cn}共有3个变号数,即变号数为3 (9分)
解法二:由题设
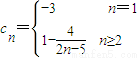
当n≥2时,令cn•cn+1<0,
得
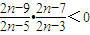 ,
,即
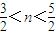 或
或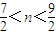 ,
,解得n=2或n=4.
又∵c1=-3,c2=5,
∴n=1时也有c1•c2<0
综上得数列{cn}共有3个变号数,即变号数为3…(9分)
(Ⅲ)n≥2且n∈N*时,


可转化为
 .
.设g(n)=
 ,
,则当n≥2且n∈N*,

=
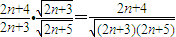
=
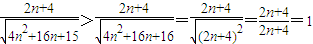 .
.所以g(n+1)>g(n),即当n增大时,g(n)也增大.
要使不等式

对于任意的n∈N*恒成立,
只需
 即可.
即可.因为
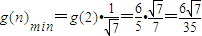 ,
,所以
 .
.即

所以,正整数m的最大值为5.(13分)
点评:本题考查数列与不等式的综合,计算量大,解题时要认真审题,注意计算能力的培养.本题对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|