题目内容
19．已知定义在R上的奇函数f（x），当x≥0时，f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，x∈[0，1]}\\{（x-2）^{2}，x∈（1，+∞）}\end{array}\right.$，若f（x）在区间[-a，a]上单调递增，则a的取值范围为（ ）| A． | （-∞，1] | B． | [1，+∞） | C． | （0，1] | D． | （-1，1] |
分析 画出函数的图象，利用已知条件列出关系式即可求出a的范围．
解答 解：定义在R上的奇函数f（x），当x≥0时，f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，x∈[0，1]}\\{（x-2）^{2}，x∈（1，+∞）}\end{array}\right.$，函数的图象如图：
f（x）在区间[-a，a]上单调递增，可得a∈（0，1]．
故选：C．
点评 本题考查分段函数的应用，函数的单调性的应用，数形结合是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
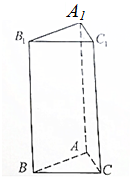已知三棱柱ABC-A1B1C1，AA1⊥平面ABC，底面ABC为正三角形，AA1=4，BC=2，延长AB至D，使BD=AB．
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（$\sqrt{3}$，0），长轴长为4．
11．设集合A={x|x2+x-6≤0}，集合B为函数$y=\frac{1}{{\sqrt{x-1}}}$的定义域，则A∩B=（ ）
| A． | （1，2） | B． | [1，2] | C． | [1，2） | D． | （1，2] |
如图，已知椭圆C中心在原点，焦点在x轴上，F1，F2分别为左右焦点，椭圆的短轴长为2，过F2的直线与椭圆C交于A，B两点，三角形F1BF2面积的最大值为$\sqrt{{a}^{2}-1}$（a＞1）．