题目内容
【题目】如图甲,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 为
为![]() ,连接
,连接![]() ,
,![]() 得到四棱锥
得到四棱锥![]() (如图乙),
(如图乙),![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上一点.
上一点.


(1)求证:当![]() 为
为![]() 的中点时,平面
的中点时,平面![]() 平面
平面![]() ;
;
(2)是否存在一点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)存在;![]()
【解析】
(1)由题易证得![]() ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,由平行线的性质可知
,由平行线的性质可知![]() 平面
平面![]() ,则
,则![]() ,再利用
,再利用![]() 可得
可得![]() ,即可求证;
,即可求证;
(2)由题以![]() 为原点,
为原点,![]() 为坐标轴建立空间坐标系
为坐标轴建立空间坐标系![]() ,设
,设![]() ,
,![]() ,分别求得平面
,分别求得平面![]() 与平面
与平面![]() 的法向量,进而利用数量积求解即可.
的法向量,进而利用数量积求解即可.
(1)证明:连接![]() ,
,![]() ,
,

由题,因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,即
,即![]() ,
,
所以![]() ,且
,且![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:存在,
以![]() 为原点,
为原点,![]() 为坐标轴建立如图所示的坐标系
为坐标轴建立如图所示的坐标系![]() ,如图所示,
,如图所示,

不妨设棱长![]() ,由(1)可知
,由(1)可知![]() 是等边三角形,
是等边三角形,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,且
,且![]() ,
,![]() ,
,
则![]() ,
,
可得![]() ,则
,则![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则 ,即
,即 ,
,
令![]() ,则
,则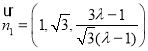 ,
,
由(1)知![]() 平面
平面![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
若存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,
则 ,
,
解得![]() ,
,
所以存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,此时
,此时![]() .
.

【题目】某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有![]() 名学生,男女生人数之比为
名学生,男女生人数之比为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下![]() 列联表:
列联表:
否定 | 肯定 | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
①完成列联表;
②能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(3)若一班有![]() 名男生被抽到,其中
名男生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度;二班有
人持肯定态度;二班有![]() 名女生被抽到,其中
名女生被抽到,其中![]() 人持否定态度,
人持否定态度,![]() 人持肯定态度.
人持肯定态度.
现从这![]() 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
解答时可参考下面临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |