题目内容
6. 如图所示,在矩形ABCD中,AB=1,AD=2,PA⊥平面ABCD,且PA=1,E,Q分别为AB,BC的中点,F在边PD上,$\overrightarrow{PF}=λ\overrightarrow{PD}$,λ∈(0,1).
如图所示,在矩形ABCD中,AB=1,AD=2,PA⊥平面ABCD,且PA=1,E,Q分别为AB,BC的中点,F在边PD上,$\overrightarrow{PF}=λ\overrightarrow{PD}$,λ∈(0,1).(1)当λ=$\frac{1}{4}$时,求证:AQ⊥EF;
(2)若平面PAQ与平面EFQ所成锐二面角的大小为60°,求λ的值.
分析 (1)以A为原点,边AB,AD,AP所在直线分别为x,y,z轴,建立空间直角坐标系,根据已知条件求出点A,Q,E,F的坐标,求数量积等于0即可;
(2)设F(0,y,z),根据条件$\overrightarrow{PF}=λ\overrightarrow{PD}$便可求得F(0,2λ,1-λ),取AQ中点M,容易判断出BM为平面PAQ的一个法向量.可设平面EFQ的法向量为$\overrightarrow{n}=({x}_{1},{y}_{1},{z}_{1})$,根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EF}=0}\\{\overrightarrow{n}•\overrightarrow{EQ}=0}\end{array}\right.$即可表示出向量$\overrightarrow{n}$的坐标,从而由平面PAQ与平面EFQ所成锐二面角的大小为60°便得到cos60°=|cos<$\overrightarrow{n},\overrightarrow{BM}$>|,这样即可建立关于λ的方程,解方程即得λ的值.
解答 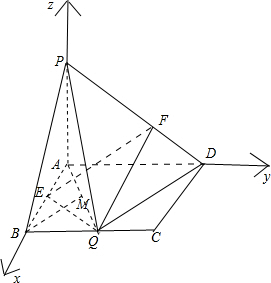 解:(1)证明:如图,以A为原点,直线AB,AD,AP分别为x,y,z轴建立空间直角坐标系,则:
解:(1)证明:如图,以A为原点,直线AB,AD,AP分别为x,y,z轴建立空间直角坐标系,则:
A(0,0,0),E($\frac{1}{2}$,0,0),Q(1,1,0),P(0,0,1),D(0,2,0),B(1,0,0);
设F(0,y,z),∴$\overrightarrow{PF}=(0,y,z-1)$,$\overrightarrow{PD}=(0,2,-1)$;
∵$\overrightarrow{PF}=\frac{1}{4}\overrightarrow{PD}$;
∴(0,y,z-1)=$\frac{1}{4}$(0,2,-1);
∴$\left\{\begin{array}{l}{y=\frac{1}{2}}\\{z=\frac{3}{4}}\end{array}\right.$;
∴$F(0,\frac{1}{2},\frac{3}{4})$;
$\overrightarrow{AQ}=(1,1,0),\overrightarrow{EF}=(-\frac{1}{2},\frac{1}{2},\frac{3}{4})$;
∴$\overrightarrow{AQ}•\overrightarrow{EF}=0$;
∴AQ⊥EF;
(2)设F(0,y,z),$\overrightarrow{PF}=λ\overrightarrow{PD}$;
∴(0,y,z-1)=λ(0,2,-1);
∴$\left\{\begin{array}{l}{y=2λ}\\{z=1-λ}\end{array}\right.$;
∴F(0,2λ,1-λ);
取AQ的中点为M,连接BM,则M($\frac{1}{2},\frac{1}{2},0$);
∵AB=BQ;
∴BM⊥AQ;
又PA⊥平面ABCD,BM?平面ABCD;
∴PA⊥BM,即BM⊥PA,PA∩AQ=A;
∴BM⊥平面PAQ;
∴$\overrightarrow{BM}$=($-\frac{1}{2},\frac{1}{2},0$)为平面PAQ的一个法向量;
设平面EFQ的法向量为$\overrightarrow{n}=({x}_{1},{y}_{1},{z}_{1})$;
则$\overrightarrow{n}⊥\overrightarrow{EF},\overrightarrow{n}⊥\overrightarrow{EQ}$;
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EF}=0}\\{\overrightarrow{n}•\overrightarrow{EQ}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{-\frac{1}{2}{x}_{1}+(2λ)•{y}_{1}+(1-λ){z}_{1}=0}\\{\frac{1}{2}{x}_{1}+{y}_{1}=0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{{x}_{1}=-2{y}_{1}}\\{{z}_{1}=\frac{1+2λ}{λ-1}{y}_{1}}\end{array}\right.$,取y1=1,则$\overrightarrow{n}=(-2,1,\frac{1+2λ}{λ-1})$;
∵平面PAQ与平面EFQ所成锐二面角的大小为60°;
∴cos60°=|cos$<\overrightarrow{n},\overrightarrow{BM}>$|=$\frac{1+\frac{1}{2}}{\sqrt{5+(\frac{1+2λ}{λ-1})^{2}}•\sqrt{\frac{1}{2}}}$;
∴解得$λ=\frac{5-\sqrt{13}}{3}$,或$λ=\frac{5+\sqrt{13}}{3}$(舍去);
即$λ=\frac{5-\sqrt{13}}{3}$.
点评 考查建立空间直角坐标系,利用空间向量证明空间异面直线垂直,解决空间角的方法,以及两非零向量垂直的充要条件,线面垂直的性质,线面垂直的判定定理,平面法向量的概念,向量数量积的坐标运算,向量夹角余弦的坐标公式,平面法向量的夹角和平面二面角的平面角度大小的关系.

| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 1 |
| A. | 奇函数,且在定义域内单调递减 | |
| B. | 奇函数,且在定义域内单调递增 | |
| C. | 非奇非偶函数,且在(0,+∞)上单调递增 | |
| D. | 偶函数,且在(0,+∞)上单调递增 |
 设 椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2是椭圆的左右焦点,以F1F2及椭圆短轴上的一个端点为顶点的三角形的面积为$\sqrt{3}$的正三角形.
设 椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2是椭圆的左右焦点,以F1F2及椭圆短轴上的一个端点为顶点的三角形的面积为$\sqrt{3}$的正三角形.