Question

设A1、A2、A3、A4、A5是空间中给定的5个不同的点，则使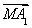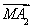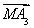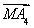＋＋＋＋＝0成立的点M的个数为________．

 

Answer 1

1个

【解析】设A1、A2、A3、A4、A5坐标分别为(x1，y1，z1)，(x2，y2，z2)，(x3，y3，z3)，(x4，y4，z4)(x5，y5，z5)，设M坐标为(x，y，z)．

由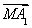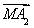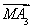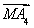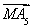＋＋＋＋＝0得方程

(x1－x)＋(x2－x)＋(x3－x)＋(x4－x)＋(x5－x)＝0，

(y1－y)＋(y2－y)＋(y3－y)＋(y4－y)＋(y5－y)＝0，

(z1－z)＋(z2－z)＋(z3－z)＋(z4－z)＋(z5－z)＝0，

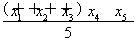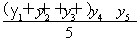解得x＝，y＝，z＝.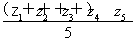

故有唯一的M满足等式．