题目内容
若函数f(x)对定义域中任意x均满足f(x)+f(2a-x)=2b,则称函数y=f(x)的图象关于点(a,b)对称.
(1)已知函数f(x)=的图象关于点(0,1)对称,求实数m的值;
(2)已知函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2+ax+1,求函数g(x)在(-∞,0)上的解析式;
(3)在(1)(2)的条件下,当t>0时,若对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,求实数a的取值范围.
【答案】
(1)由题设可得f(x)+f(-x)=2,
即+=2,解得m=1.
(2)当x<0时,-x>0且g(x)+g(-x)=2,
∴g(x)=2-g(-x)=-x2+ax+1.
(3)由(1)得f(t)=t++1(t>0),
其最小值为f(1)=3.
g(x)=-x2+ax+1=-2+1+,
①当<0,即a<0时,g(x)max=1+<3,
得a∈(-2,0)
②当≥0,即a≥0时,g(x)max<1<3,
得a∈[0,+∞);由①②得a∈(-2,+∞)
【解析】略

练习册系列答案
相关题目
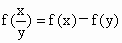 ,则不等式f(x+b)-f
,则不等式f(x+b)-f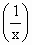 <2f(4)的解为
<2f(4)的解为