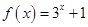题目内容
函数 的定义域为
的定义域为 ,若
,若

 ,且
,且 时总有
时总有 ,则称
,则称 为单函数.例如
为单函数.例如 是单函数,现给出下列结论:
是单函数,现给出下列结论:
①函数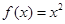
 是单函数;
是单函数;
②函数 是单函数;
是单函数;
③偶函数 ,
, (
( )有可能是单函数;
)有可能是单函数;
④在定义域上具有单调性的函数一定是单函数.
其中的正确的结论是 (写出所有正确结论的序号).
②④
解析试题分析:因为根据题意 为单函数,说明一个x对应一个y,反之呢,一个y对应一个x,因此根据对于概念的理解, 得到
为单函数,说明一个x对应一个y,反之呢,一个y对应一个x,因此根据对于概念的理解, 得到
命题1中,函数是二次函数,显然不满足一个y对应一个x。舍去
命题2中,是指数函数,在整个定义域内严格递增,那么满足单函数的定义,成立。
命题3中,由于函数是抽象函数,且为偶函数 ,
, (
( )有可能是单函数,不能满足。因为f(-m)=f(m),不同的变量也有同一个函数值。故错误
)有可能是单函数,不能满足。因为f(-m)=f(m),不同的变量也有同一个函数值。故错误
命题4中,在定义域上具有单调性的函数一定是单函数.
显然符合定义,故成立,正确的命题序号为②④
考点:本试题考查了新定义的运用。
点评:理解这里的单函数实际上就是一一对应的函数,那么利用这一点逐项分析,结合指数函数和幂函数的性质来得到结论。属于中档题。

练习册系列答案
相关题目
 :函数
:函数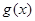 =
= 是
是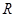 上的减函数,命题
上的减函数,命题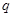 :函数
:函数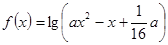 的定义域为
的定义域为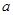 的取值范围.
的取值范围. 的定义域为
的定义域为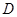 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的
上的 的函数
的函数 为
为 高调函数,那么实数
高调函数,那么实数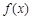 的定义域为
的定义域为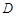 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
;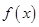 的定义域为
的定义域为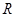 ,若存在常数
,若存在常数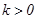 ,使
,使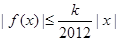 对一切实数
对一切实数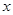 均成立,则称
均成立,则称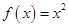 ;②
;② ;③
;③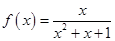 ;④
;④