题目内容
设函数 的定义域为
的定义域为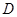 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为
为 上的
上的 高调函数.如果定义域是
高调函数.如果定义域是 的函数
的函数 为
为 上的
上的 高调函数,那么实数
高调函数,那么实数 的取值范围是 .
的取值范围是 .
【答案】
m≥2
【解析】)∵定义域是[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,∴当x≥-1时,x+m≥m-1≥-1∴m≥0,而m≠0,∴m>0.又函数f(x)=x2为[-1,+∞)上的m高调函数,∴f(x+m)≥f(x),即(x+m)2≥x2,∴2mx+m2≥0,又m>0,∴m≥-2x(x≥-1)恒成立,∴m≥(-2x)max,由x≥-1可得-x≤1,-2x≤2,∴(-2x)max=2,∴m≥2.
故答案为:m≥2.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 的定义域为
的定义域为 ,若满足:①
,若满足:①
 ,使得
,使得 上的值域为
上的值域为 是定义域为
是定义域为 是定义域为
是定义域为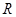 的“成功函数”,则
的“成功函数”,则 的取值范围为 ( )
的取值范围为 ( )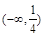 B.
B.
 C.
C.
 D.
D.

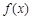 的定义域为
的定义域为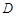 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
; 的定义域为
的定义域为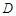 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的“
上的“ 高调函数”.现给出下列命题:
高调函数”.现给出下列命题: 为
为 上的“1高调函数”;
上的“1高调函数”; 为
为 高调函数”;
高调函数”; 的函数
的函数 为
为 高调函数”,那么实数
高调函数”,那么实数 ;
;