题目内容
已知命题1+2+22+…+2n-1=2n-1及其证明：
（1）当n=1时，左边=1，右边=21-1=1，所以等式成立；
（2）假设n=k时等式成立，即1+2+22+…+2k-1=2k-1 成立，
则当n=k+1时，1+2+22+…+2k-1+2k=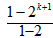
=2k+1-1，所以n=k+1时等式也成立，
由（1）（2）知，对任意的正整数n等式都成立，
判断以上评述
（1）当n=1时，左边=1，右边=21-1=1，所以等式成立；
（2）假设n=k时等式成立，即1+2+22+…+2k-1=2k-1 成立，
则当n=k+1时，1+2+22+…+2k-1+2k=
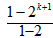=2k+1-1，所以n=k+1时等式也成立，由（1）（2）知，对任意的正整数n等式都成立，
判断以上评述
[ ]
A.命题、推理都正确
B.命题正确、推理不正确
C.命题不正确、推理正确
D.命题、推理都不正确
B.命题正确、推理不正确
C.命题不正确、推理正确
D.命题、推理都不正确
B
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目