题目内容
已知命题P:直线x+y-2=0与圆(x-a)2-(y-a)2=2相切;命题Q:f (x)=log(2a-1)x在(0,+∞)上为增函数,若P∧Q为真命题,则a=
2
2
.分析:由P∧Q为真命题,知命题P和命题Q都是真命题.由命题P:直线x+y-2=0与圆(x-a)2-(y-a)2=2相切是真命题,解得a=2,或a=0.由命题Q:f (x)=log(2a-1)x在(0,+∞)上为增函数是真命题,解得a>1.由此能求出a的值.
解答:解:∵P∧Q为真命题,
∴命题P和命题Q都是真命题.
∵命题P:直线x+y-2=0与圆(x-a)2-(y-a)2=2相切是真命题,
∴
=
,解得a=2,或a=0.
∵命题Q:f (x)=log(2a-1)x在(0,+∞)上为增函数是真命题,
∴2a-1>1,解得a>1.
∴a=2.
故答案为2.
∴命题P和命题Q都是真命题.
∵命题P:直线x+y-2=0与圆(x-a)2-(y-a)2=2相切是真命题,
∴
| |a+a-2| | ||
|
| 2 |
∵命题Q:f (x)=log(2a-1)x在(0,+∞)上为增函数是真命题,
∴2a-1>1,解得a>1.
∴a=2.
故答案为2.
点评:本题考查命题的真假判断与应用,是基础题.解题时要认真审题,仔细解答,注意点到直线距离公式的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
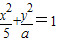 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.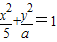 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.