题目内容
设角A,B,C是△ABC的三个内角,已知向量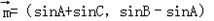 ,
,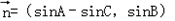 ,且
,且 .
.
(Ⅰ)求角C的大小;
(Ⅱ)若向量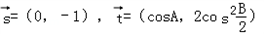 ,试求
,试求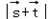 的取值范围.
的取值范围.
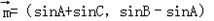 ,
,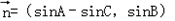 ,且
,且 .
.(Ⅰ)求角C的大小;
(Ⅱ)若向量
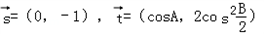 ,试求
,试求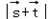 的取值范围.
的取值范围.解:(Ⅰ)由题意得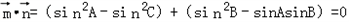
即sin2C=sin2A+sin2B﹣sinAsinB
由正弦定理得c2=a2+b2﹣ab
再由余弦定理得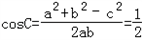
∵0<C<π,
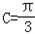
∴
(Ⅱ)∵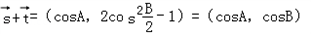
∴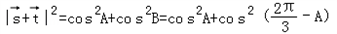
=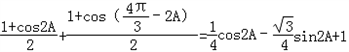
=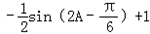
∵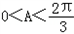 ,
,
∴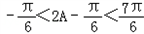
∴
所以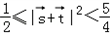 ,
,
故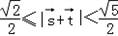 .
.
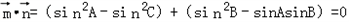
即sin2C=sin2A+sin2B﹣sinAsinB
由正弦定理得c2=a2+b2﹣ab
再由余弦定理得
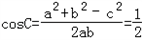
∵0<C<π,
∴

(Ⅱ)∵
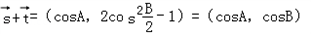
∴
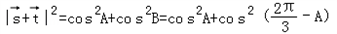
=
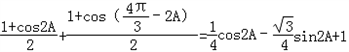
=
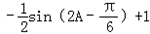
∵
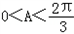 ,
,∴
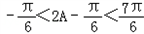
∴

所以
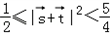 ,
,故
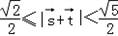 .
.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
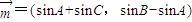 ,
,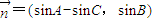 ,且
,且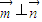 .
. ,试求
,试求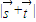 的取值范围.
的取值范围.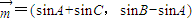 ,
,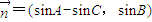 ,且
,且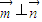 .
. ,试求
,试求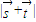 的取值范围.
的取值范围.