题目内容
设角A,B,C是△ABC的三个内角,已知向量| m |
| n |
| m |
| n |
(Ⅰ)求角C的大小;
(Ⅱ)若向量
| s |
| t |
| B |
| 2 |
| s |
| t |
分析:(Ⅰ)根据
⊥
推断出
•
=0,利用向量的基本运算求得sin2C=sin2A+sin2B-sinAsinB,利用正弦定理把角的正弦转化成边,代入余弦定理求得cosC的值,进而求得C.
(Ⅱ)根据
和
的坐标可求得|
+
|2的表达式,然后利用二倍角公式化简整理,利用A的范围和正弦函数的单调性求得|
+
|2的范围,进而求得|
+
|的取值范围.
| m |
| n |
| m |
| n |
(Ⅱ)根据
| s |
| t |
| s |
| t |
| s |
| t |
| s |
| t |
解答:解:(Ⅰ)由题意得
•
=(sin2A-sin2C)+(sin2B-sinAsinB)=0
即sin2C=sin2A+sin2B-sinAsinB
由正弦定理得c2=a2+b2-ab
再由余弦定理得cosC=
=
∵0<C<π,∴C=
(Ⅱ)∵
+
=(cosA,2cos2
-1)=(cosA,cosB)
∴|
+
|2=cos2A+cos2B=cos2A+cos2(
-A)
=
+
=
cos2A-
sin2A+1
=-
sin(2A-
)+1
∵0<A<
,∴-
<2A-
<
∴-
<sin(2A-
)≤1
所以
≤|
+
|2<
,故
≤|
+
|<
.
| m |
| n |
即sin2C=sin2A+sin2B-sinAsinB
由正弦定理得c2=a2+b2-ab
再由余弦定理得cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵0<C<π,∴C=
| π |
| 3 |
(Ⅱ)∵
| s |
| t |
| B |
| 2 |
∴|
| s |
| t |
| 2π |
| 3 |
=
| 1+cos2A |
| 2 |
1+cos(
| ||
| 2 |
| 1 |
| 4 |
| ||
| 4 |
=-
| 1 |
| 2 |
| π |
| 6 |
∵0<A<
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
所以
| 1 |
| 2 |
| s |
| t |
| 5 |
| 4 |
| ||
| 2 |
| s |
| t |
| ||
| 2 |
点评:本题主要考查了正弦定理和余弦定理的应用,向量的基本运算,三角函数的基本公式.综合考查了学生对基础知识整体把握.

练习册系列答案
相关题目
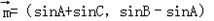 ,
,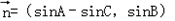 ,且
,且 .
.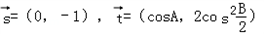 ,试求
,试求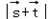 的取值范围.
的取值范围.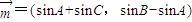 ,
,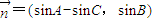 ,且
,且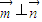 .
. ,试求
,试求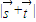 的取值范围.
的取值范围.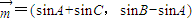 ,
,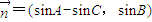 ,且
,且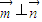 .
. ,试求
,试求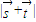 的取值范围.
的取值范围.