��Ŀ����
(��С������12��)�жԳ����ĵ����߽��������ߣ���Բ����Բ��˫���߶����������ߣ����������ߵ����ĵ��ҽ��������ߵ�ֱ���������������������Ƶ��������ʡ�
��1����������Բ![]() ������ֱ�����˵������һ����ֱ�����˵������б��֮��Ϊ��ֵ
������ֱ�����˵������һ����ֱ�����˵������б��֮��Ϊ��ֵ![]() ����д���ö�������Բ
����д���ö�������Բ![]() �е����ƽ��ۣ�
�е����ƽ��ۣ�
��2��������Բ![]() ���������ഹֱ��ֱ����Ϊ����ֱ����������������ֱ����Բ�ཻ�õ����ı��ε����Ϊ��ֵ
���������ഹֱ��ֱ����Ϊ����ֱ����������������ֱ����Բ�ཻ�õ����ı��ε����Ϊ��ֵ![]() ������Բ������б��֮��Ϊ
������Բ������б��֮��Ϊ![]() ��ֱ����Ϊ����ֱ������̽����Բ
��ֱ����Ϊ����ֱ������̽����Բ![]() ����������ֱ������Բ�ཻ�õ����ı��ε���������ƽ��ۣ�������֤����
����������ֱ������Բ�ཻ�õ����ı��ε���������ƽ��ۣ�������֤����
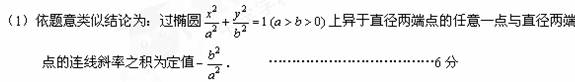
��2����������Բ�������ƶ�����
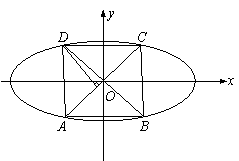 ��Բ
��Բ![]() ������ֱ����б��֮��Ϊ
������ֱ����б��֮��Ϊ![]() ʱ����Ϊ����ֱ�����ر�أ���һ��ֱ����б�ʲ����ڣ���һ��ֱ����б��Ϊ��ʱҲ��Ϊ����ֱ������������ֱ������Բ�ཻ�õ����ı��ε����Ϊ��ֵ2ab�� ������������������������������������������������8��
ʱ����Ϊ����ֱ�����ر�أ���һ��ֱ����б�ʲ����ڣ���һ��ֱ����б��Ϊ��ʱҲ��Ϊ����ֱ������������ֱ������Բ�ཻ�õ����ı��ε����Ϊ��ֵ2ab�� ������������������������������������������������8��
֤�����ٵ���������ֱ��Ϊ��Բ�ij�����ʱ����Ӧ���ı������Ϊ2ab�������� 9��
��һ��أ�����ֱ��AC��б��Ϊk������ֱ��BD��б��Ϊ![]() ��k��0����
��k��0����
��A��x1��y1����C��x2��y2����
![]() ��
�� 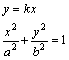
![]() ��
��
![]() ��
��
ͬ���ɵ� ![]() ��
��
D��ֱ��AC�ľ���Ϊ![]() ��
��
��S�ı���ABCD��|AC|��d��![]() Ϊ��ֵ. ������12��
Ϊ��ֵ. ������12��
