题目内容
设函数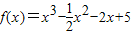 ,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )
,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )A.(7,+∞)
B.(8,+∞)
C.[7,+∞)
D.(9,+∞)
【答案】分析:由题意先对函数y进行求导,解出极值点,然后再根据函数的定义域,把极值点和区间端点值代入已知函数,比较函数值的大小,求出最大值,从而求解.
解答:解:∵f(x)<m恒成立,即f(x)的最大值<m恒成立,
∴f′(x)=3x2-x-2,
当x∈[-1,- ]时f(x)为增函数,
]时f(x)为增函数,
当x∈[- ,1]时,f(x)为减函数,
,1]时,f(x)为减函数,
∴f(x)的最大值为f(2)=7,
所以m的取值范围为(7,+∞).
故选A.
点评:此题是一道常见的题型,把函数的最值和不等式的恒成立联系起来出题,对这样的题要注意,用导数求函数的最值.
解答:解:∵f(x)<m恒成立,即f(x)的最大值<m恒成立,
∴f′(x)=3x2-x-2,
当x∈[-1,-
 ]时f(x)为增函数,
]时f(x)为增函数,当x∈[-
 ,1]时,f(x)为减函数,
,1]时,f(x)为减函数,∴f(x)的最大值为f(2)=7,
所以m的取值范围为(7,+∞).
故选A.
点评:此题是一道常见的题型,把函数的最值和不等式的恒成立联系起来出题,对这样的题要注意,用导数求函数的最值.

练习册系列答案
相关题目
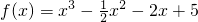 ,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为
,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为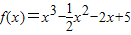 ,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )
,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( ) ,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )
,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )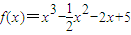 ,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )
,若对于任意x∈[-1,2]都有f(x)<m成立,则实数m的取值范围为( )