题目内容
当0<a<1时,解关于x的不等式a| 2x-1 |
分析:由0<a<1,根据指数函数的单调性,原不等式可化为
>x-2然后分x-2<0和x-2≥0两种情况,通过平方转化为有理不等式求解,最后两种情况取并集.
| 2x-1 |
解答:解:由0<a<1,原不等式可化为
>x-2
这个不等式的解集是下面不等式组(1)及(2)的解集的并集:
(1)或
(2)
解不等式组(1)得解集{x|
≤x<2}解不等式组(2)得解集{x|2≤x<5}
所以原不等式的解集为:{x|
≤x<5}
| 2x-1 |
这个不等式的解集是下面不等式组(1)及(2)的解集的并集:
|
|
解不等式组(1)得解集{x|
| 1 |
| 2 |
所以原不等式的解集为:{x|
| 1 |
| 2 |
点评:本题主要考查不等式的解法、指数函数的性质等基本知识,考查运算能力和逻辑思维能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.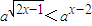 .
.