题目内容
(本小题满分12分)
 如图,四棱锥P-ABCD的底面为矩形,侧棱PD垂直于底面,PD=DC=2BC,E为棱PC上的点,且平面BDE⊥平面PBC.
如图,四棱锥P-ABCD的底面为矩形,侧棱PD垂直于底面,PD=DC=2BC,E为棱PC上的点,且平面BDE⊥平面PBC.
(1)求证:E为PC的中点;
(2)求二面角A-BD-E的大小.
解法一:(1)证明:如图,作CF⊥BE,垂足为F,
由平面BDE⊥平面PBC,
则CF⊥平面BDE,知CF⊥DE.
因为PD⊥平面ABCD,BC⊥CD,
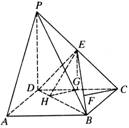 CD为DE在平面ABCD内的射影,
CD为DE在平面ABCD内的射影,
所以BC⊥DE,所以DE⊥平面PBC.
于是DE⊥PC,又PD=PC,所以E为PC的中点.………………6分
(2)作EG⊥DC,垂足为G,则EG∥PD,从而EG⊥平面ABCD.
作GH⊥BD,垂足为H,连接EH,则BD⊥EH,
故∠EHG为二面角A-BD-E的平面角的补角.…………………9分
不妨设BC=1,则PD=DC=2,
在Rt△EGH中,EG=![]() PD=1,
PD=1,
GH=![]() =
=![]() ,
,
∴tan∠EHC=![]() =
=![]() .
.
因此二面角A-BD-E的大小为![]() -arctan
-arctan![]() .……………………12分
.……………………12分
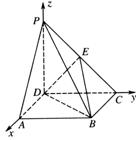 解法二:不妨设BC=1,则PD=DC=2.
解法二:不妨设BC=1,则PD=DC=2.
建立如图所示的空间直角坐标系D-xyz,
则D(0,0,0),B(1,2,0),C(0,2,0),P(0,0,2).
(1)证明:设![]() =
=![]() ,则E(0,
,则E(0,![]() ,
,![]() ).
).
设a= (x1,y1,z1)为面PBC的法向量,
则a⊥![]() ,a⊥
,a⊥![]() ,
,
又![]() =(1,0,0),
=(1,0,0),![]() =(0,-2,2),
=(0,-2,2),
∴a![]() =x1=0,a
=x1=0,a![]() =-2y1+2z1=0,
=-2y1+2z1=0,
取a=(0,1,1).
设b=(x2,y2,z2)为面BDE的法向量,
则b⊥![]() ,b⊥
,b⊥![]() ,
,
又![]() =(1,2,0),
=(1,2,0),![]() =(0,
=(0,![]() ,
,![]() ),
),
∴b![]() =x2+2y2=0,b
=x2+2y2=0,b![]() =
=![]() +
+![]() =0,
=0,
取b=(![]() ,
,![]() ,1).
,1).
∵平面BDE⊥平面PBC,
∴a·b=![]() +1=0,
+1=0,![]() =1.
=1.
所以E为PC的中点.…………………………………………6分
(2)由(Ⅰ)知,b=(2,-1,1)为面BDE的法向量,
又c=(0,0,1)为面ADB的法向量,
∵cos<b,c>=![]() =
=![]() ,
,
所以二面角A-BD-E的大小为![]() -arccos
-arccos![]() .………………12分
.………………12分
