题目内容
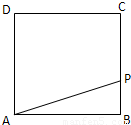
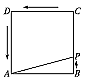
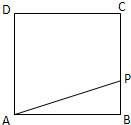 如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,
如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,(I) 求y关于x的解析式,
(II) 求x=2时,y的值.
分析:(I) 由题意及图形知y关于x的解析式要分段来求,由图形知可分为四段求函数的解析;
(II) x=2时,代入(I)中相应的函数解析式,求的值
(II) x=2时,代入(I)中相应的函数解析式,求的值
解答: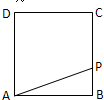 解:(I)依题意可知函数的定义域为[0,4]. …(1分)
解:(I)依题意可知函数的定义域为[0,4]. …(1分)
当x∈[0,1)时,y=x;…3,
当x∈[1,2)时,y=
;…5,
当x∈[2,3)时,y=
;…7,
当x∈[3,4]时,y=4-x.…9,
故y关于x的解析式为y=
…(11分)
(II) 当x=2时,y=
=
.…(14分)
 解:(I)依题意可知函数的定义域为[0,4]. …(1分)
解:(I)依题意可知函数的定义域为[0,4]. …(1分)当x∈[0,1)时,y=x;…3,
当x∈[1,2)时,y=
| (x-1)2+1 |
当x∈[2,3)时,y=
| (3-x)2+1 |
当x∈[3,4]时,y=4-x.…9,
故y关于x的解析式为y=
|
(II) 当x=2时,y=
| (3-2)2+1 |
| 2 |
点评:本题考查分段函数的解析式求法及其图象的作法,解答本题关键是根据实际问题将函数的解析式分成几段求解,建立分段函数模型,分段函数是一个非常重要的函数模型,适应范围广泛,注意体会本题中的分类思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
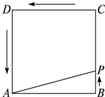 如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C、D、A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C、D、A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.