题目内容
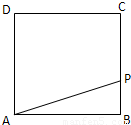
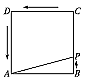
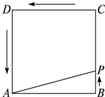 如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C、D、A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C、D、A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.分析:△APB的形状各有特征,计算它们的面积也有不同的方法,因此同样必须对P点的位置进行分类求解即可.
解答:解:当点P在BC上运动,即0≤x≤4时,y=
×4x=2x;
当点P在CD上运动,即4<x≤8时,y=
×4×4=8;
当点P在DA上运动,即8<x≤12时,y=
×4×(12-x)=24-2x.
综上可知,f(x)=
| 1 |
| 2 |
当点P在CD上运动,即4<x≤8时,y=
| 1 |
| 2 |
当点P在DA上运动,即8<x≤12时,y=
| 1 |
| 2 |
综上可知,f(x)=
|
点评:本题主要考查了分段函数式的求法,背景是动点的轨迹特征不同,三角形的面积也会随着变化,其中蕴藏着函数的思想方法,属于中档题.

练习册系列答案
相关题目
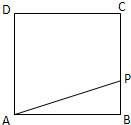 如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,
如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,