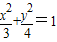题目内容
已知椭圆两个焦点的坐标分别是(-1,0),(1,0),并且经过点(2,0),则它的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:设出椭圆方程,将点的坐标代入,求出a的值;根据椭圆中三个参数的关系求出b,代入椭圆方程即可.
解答:解:设椭圆的方程为
+
=1
将(2,0)代入得a2=4
∵椭圆两个焦点的坐标分别是(-1,0),(1,0),
∴c2=1
∴b2=a2-c2=3
∴椭圆的方程为
+
=1
故选D
| x2 |
| a2 |
| y2 |
| b2 |
将(2,0)代入得a2=4
∵椭圆两个焦点的坐标分别是(-1,0),(1,0),
∴c2=1
∴b2=a2-c2=3
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
故选D
点评:求圆锥曲线的方程的问题,一般利用待定系数法;注意椭圆中三个参数的关系为b2=a2-c2而双曲线中三个参数的关系为b2=c2-a2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目