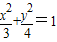题目内容
已知椭圆两个焦点的坐标分别是(-1,0),(1,0),并且经过点(2,0),它的标准方程为分析:先判断椭圆的焦点位置,求出半焦距,经过点(2,0)的椭圆的长半轴等于2,可求短半轴,从而写出椭圆的标准方程.
解答:解:由题意知,椭圆的焦点在x轴上,c=1,a=2,∴b2=3,
故椭圆的方程为为
+
=1
故答案为:
+
=1.
故椭圆的方程为为
| x2 |
| 4 |
| y2 |
| 3 |
故答案为:
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题考查椭圆的性质及标准方程的求法,用待定系数法求椭圆的标准方程是一种常用的方法.

练习册系列答案
相关题目
已知椭圆两个焦点的坐标分别是(-1,0),(1,0),并且经过点(2,0),则它的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|