题目内容
函数f(x)=Msin(ωx+φ)(ω>0)在区间[a,b]上是增函数,且f(b)=M,f(a)=-M,则函数g(x)=Mcos(ωx+φ)在区间[a,b]上( )
| A.是增函数 |
| B.是减函数 |
| C.可取得最大值M |
| D.可取得最小值-M |
C
解析试题分析:∵函数f(x)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M
∴M>0且区间[a,b]关于原点对称, 从而函数函数f(x)为奇函数φ=2kπ, 。
。
∴函数g(x)=Mcos(ωx+φ)=Mcoswx在区间[a,0]是增函数,[0,b]减函数,
∴函数g(x)=Mcos(ωx+φ)在区间[a,b]上取得最大值M,故选C.
考点:正弦函数、余弦函数的图象及性质
点评:中档题,本题利用整体思想,研究函数的单调性,在解题过程中,熟练运用相关结论:y=Asin(wx+φ)为奇(偶)函数⇒φ=kπ(φ=kπ+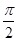 )(k∈Z),是解题的关键。
)(k∈Z),是解题的关键。

练习册系列答案
相关题目
已知 ,则
,则 ( )
( )
A.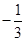 | B. | C. | D. |
函数 的最小正周期是 ( )
的最小正周期是 ( )
A. | B. | C. | D. |
函数 (
( )的单调递增区间是( ).
)的单调递增区间是( ).
A. | B. | C. | D. |
已知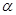 为第三象限角,则
为第三象限角,则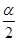 所在的象限是( )
所在的象限是( )
| A.第一或第二象限 | B.第二或第三象限 | C.第一或第三象限 | D.第二或第四象限角 |
已知函数 在
在 上单调递减,则
上单调递减,则 的取值范围
的取值范围
A. | B.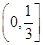 | C. | D. |
把函数 的图象按向量
的图象按向量 平移,得到函数
平移,得到函数 的图象,则
的图象,则 可以是:( )
可以是:( )
A.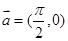 | B. | C. | D. |
已知函数, 下面结论错误的是( )
下面结论错误的是( )
A.函数 的最小正周期为 的最小正周期为 | B.函数 是奇函数 是奇函数 |
C.函数 的图象关于直线 的图象关于直线  =0对称 =0对称 | D.函数 在区间 在区间 上是增函数 上是增函数 |
(5分)函数 的部分图象如图所示,则ω,φ的值分别是( )
的部分图象如图所示,则ω,φ的值分别是( )
A. | B. | C. | D. |