题目内容
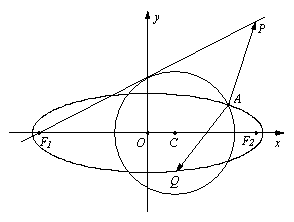
（本小题满分15分）已知点P（4，4），圆C：
与椭圆E：
有一个公共点A（3，1），F1．F2分别
是椭圆的左．右焦点，直线PF1与圆C相切．
（1）求m的值与椭圆E的方程；
（2）设Q为椭圆E上的一个动点，求
的范围．
解：（Ⅰ）点A代入圆C方程， 得
． ∵m＜3，∴m＝1．
圆C：
．设直线PF1的斜率为k，
则PF1：
，即
．
∵直线PF1与圆C相切，∴
．
解得
．当k＝
时，直线PF1与x轴的交点横坐标为
，不合题意舍去．
当k＝
时，直线PF1与x轴的交点横坐标为－4，
∴c＝4．F1（－4，0），F2（4，0）．2a＝AF1＋AF2＝
，
，a2＝18，
b2＝2．椭圆E的方程为：
．
（Ⅱ）
，设Q（x，y），
，
．∵，即
，
而
，∴－18≤6xy≤18．
则
的取值范围是[0，36]．
的取值范围是[－6，6]．
∴
的取值范围是[－12，0]．
练习册系列答案
名校课堂系列答案
相关题目
的单调区间；
，试分别解答以下两小题.
对任意的
恒成立，求实数
的取值范围；
是两个不相等的正数，且
，求证：
．
、
分别为椭圆
：
的 
：
的焦点，
是
。
：
，过点P的动直线
与圆
，
（
且
）。求证：点Q总在某定直线上。
的左、右焦点分别为
、
，过
与椭圆相交于A、B两点。
，且
，求椭圆的离心率；
求
的最大值和最小值。
在定义域内存在区间
，满足
是否为“优美函数”？若是，求出
；若不是，说明理由；
为“优美函数”，求实数
的取值范围．