Question

（08年长沙一中一模文）如图，已知、为平面上的两个定点，为动点，

且（是和的交点）。

       （1）建立适当的平面直角坐标系求出点的轨迹方程；

       （2）若点的轨迹上存在两个不同的点A、B，且线段AB的中垂线与（或的延长线）相交于一点，证明：（为的中点）。

 

Answer 1

解析：（1）如图1，以所在的直线为轴，的中垂线为轴，建立平面直角坐标系

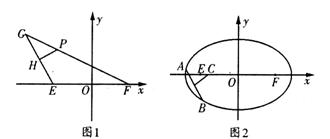
       由题设，而

       点是以、为焦点，长轴长为10的椭圆，

       故点的轨迹方程为（6分）

       （2）解法一：如图2，设，，且，

       即，又A、B在轨迹上，

       即

       代入整理得： （10分）

      

       即 （13分）

 

解法二：设，及中点坐标为，

       则、在轨迹上，，]

       两式相减得，

       的中垂线的方程为，令得。

       即，又（13分）