题目内容
(12分) 函数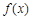 对任意
对任意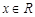 都有
都有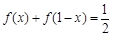 .
.
(1)
求 和
和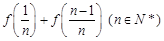 的值;
的值;
(2)
数列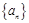 满足:
满足: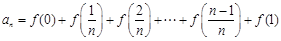 ,数列{an}是等差数列吗?请给予证明;
,数列{an}是等差数列吗?请给予证明;
(3)
在第(2)问的条件下,若数列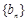 满足
满足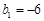 ,
,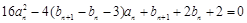 ,试求数列
,试求数列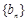 的通项公式.
的通项公式.
【答案】
解:(1) 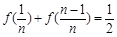 .(2)
.(2) 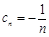 ,∴
,∴
【解析】本试题主要是考查了数列与函数、不等式的综合的运用。
(1) 因为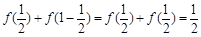 .所以
.所以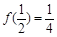
令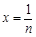 ,即
,即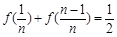 .
.
(2)因为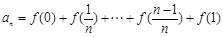 结合上一问的结论,可知
结合上一问的结论,可知
又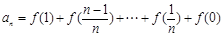
两式相加得. 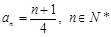 ,又
,又 .
.
故数列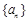 是等差数列
是等差数列
(3) 由(2)知,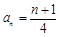 ,代入
,代入
整理得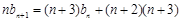 构造
构造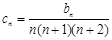 得到其通项公式。
得到其通项公式。
解:(1) 因为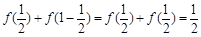 .所以
.所以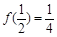 .·········· 2分
.·········· 2分
令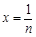 ,得
,得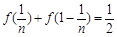 ,即
,即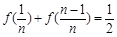 .············· 4分
.············· 4分
(2)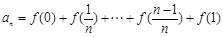
又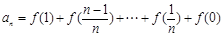
两式相加得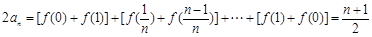 .
.
所以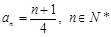 ,又
,又 .
.
故数列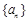 是等差数列.··························· 8分
是等差数列.··························· 8分
(3) 由(2)知,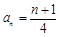 ,代入
,代入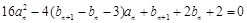
整理得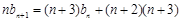
两边同除以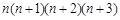 ,得
,得
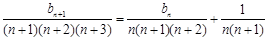
令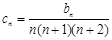 ,则
,则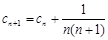 ,且
,且
累加得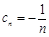 ,∴
,∴ ····················· 12分
····················· 12分

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的定义域为
的定义域为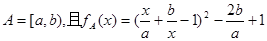 ,其中a、b为任
,其中a、b为任 时,研究
时,研究 其中k是正整数,对一切正整数k不等式
其中k是正整数,对一切正整数k不等式 都有解,求m的取值范围。
都有解,求m的取值范围。 、
、 、
、 满足
满足 ,则称
,则称 比3接近0,求
比3接近0,求 、
、 ,证明:
,证明: 比
比 接近
接近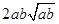 ;
; 的定义域
的定义域 .任取
.任取 ,
, 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数