题目内容
(本题满分14分)如图,在平行六面体ABCD-A1BC1D1中,
已知: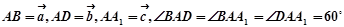 ,且
,且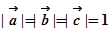 ,O是B1D1的中点.
,O是B1D1的中点.
(1)求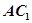 的长;
的长;
(2)求异面直线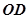 与
与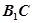 所成角的余弦值.
所成角的余弦值.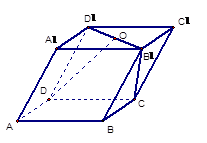
已知:
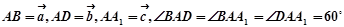 ,且
,且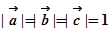 ,O是B1D1的中点.
,O是B1D1的中点.(1)求
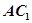 的长;
的长;(2)求异面直线
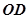 与
与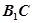 所成角的余弦值.
所成角的余弦值.
(1)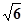 ;(2)
;(2)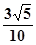 .
.
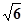 ;(2)
;(2)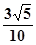 .
.第一问利用已知的空间向量基本定理,表示体对角线的向量,然后利用数量积的性质,模的平方等于向量的平方,得到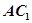 的长度
的长度
第二问中,分别表示异面直线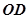 与
与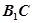 所在的向量的坐标,通过求解向量的数量积来表示夹角,从而得到结论。
所在的向量的坐标,通过求解向量的数量积来表示夹角,从而得到结论。
(1)解:设 AB =" a" , AD =" b" , AA1 =" c" ,则两两夹角为60°,且模均为1.
(1) AC1 =" AC" + CC1 =" AB" + AD + AA1 =" a" + b + c .
∴| AC1 |2=( a + b + c )2="|" a |2+| b |2+| c |2+2 a • b +2 b • c +2 a • c=3+6×1×1×1 2 =6,
∴| AC1 |=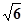 ,即AC1的长为
,即AC1的长为 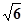 . ………………6分
. ………………6分
(2)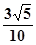 ………………14分
………………14分
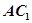 的长度
的长度第二问中,分别表示异面直线
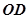 与
与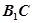 所在的向量的坐标,通过求解向量的数量积来表示夹角,从而得到结论。
所在的向量的坐标,通过求解向量的数量积来表示夹角,从而得到结论。(1)解:设 AB =" a" , AD =" b" , AA1 =" c" ,则两两夹角为60°,且模均为1.
(1) AC1 =" AC" + CC1 =" AB" + AD + AA1 =" a" + b + c .
∴| AC1 |2=( a + b + c )2="|" a |2+| b |2+| c |2+2 a • b +2 b • c +2 a • c=3+6×1×1×1 2 =6,
∴| AC1 |=
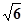 ,即AC1的长为
,即AC1的长为 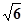 . ………………6分
. ………………6分 (2)
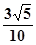 ………………14分
………………14分
练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 ,则点A到平面
,则点A到平面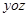 的距离为___.
的距离为___.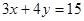 上,则
上,则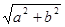 的最小值为
的最小值为 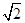
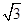
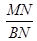 取最小值时,
取最小值时,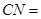 _________。
_________。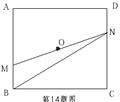
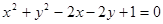 上的点到直线
上的点到直线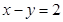 的距离最大值是
的距离最大值是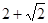
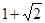
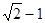
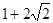
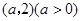 直线
直线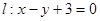 的距离为1,则a=________
的距离为1,则a=________