题目内容
【题目】在海岸A处，发现北偏东45°方向，距A处（ 
﹣1）海里的B处有一艘走私船，在A处北偏西75°方向，距A处2海里的C处的缉私船奉命以10 海里/小时的速度追截走私船，此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜，问缉私船沿什么方向能最快追上走私船，并求出所需要的时间． 
【答案】解：如图所示，设缉私船追上走私船需t小时， 则有CD= 
，BD=10t．在△ABC中，
∵AB= 
﹣1，AC=2，
∠BAC=45°+75°=120°．
根据余弦定理可求得BC= 
．
∠CBD=90°+30°=120°．
在△BCD中，根据正弦定理可得
sin∠BCD= 
，
∵∠CBD=120°，∴∠BCD=30°，∠BDC=30°，
∴BD=BC= ，则有
10t= ，t= 
=0.245（小时）=14.7（分钟）．
所以缉私船沿北偏东60°方向，需14.7分钟才能追上走私船．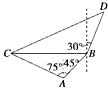
【解析】设缉私船追上走私船需t小时，进而可表示出CD和BD，进而在△ABC中利用余弦定理求得BC，进而在△BCD中，根据正弦定理可求得sin∠BCD的值，进而求得∠BDC=∠BCD=30°进而求得BD，进而利用BD=10t求得t．
练习册系列答案
相关题目
【题目】对一批共50件的某电器进行分类检测，其重量（克）统计如下：
质量段 | [80，85） | [85，90） | [90，95） | [95，100] |
件数 | 5 | a | 15 | b |
规定重量在82克及以下的为“A”型，重量在85克及以上的为“B”型，已知该批电器有“A“型2件
（1）从该批电器中任选1件，求其为“B”型的概率；
（2）从重量在[80，85）的5件电器中，任选2件，求其中恰有1件为“A”型的概率．
