题目内容
7个人排成一排,按下列要求各有多少种排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙、丙3人必须相邻;
(3)其中甲、乙、丙3人两两不相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲、乙、丙按从左到右的顺序排列.
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙、丙3人必须相邻;
(3)其中甲、乙、丙3人两两不相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲、乙、丙按从左到右的顺序排列.
(1)3720种 (2)720种 (3)1440种 (4)1200种 (5)840种
(1)方法一(直接法):如果甲站排尾,其余6人有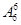 种排法,如果甲站中间5个位置中的一个,而乙不站排尾,则有
种排法,如果甲站中间5个位置中的一个,而乙不站排尾,则有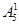
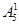
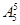 种排法,故共有排法
种排法,故共有排法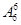 +
+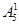
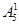
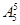 =3720种.
=3720种.
方法二(间接法):7个人排成一排有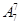 种排法,其中甲在排头有
种排法,其中甲在排头有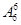 种排法,乙在排尾有
种排法,乙在排尾有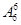 种排法,甲在排头且乙在排尾共有
种排法,甲在排头且乙在排尾共有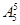 种排法,故共有排法
种排法,故共有排法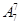 -
-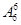 -
-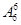 +
+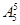 =3720种.
=3720种.
(2)(捆绑法)将甲、乙、丙捆在一起作为一个元素与其他4个元素作全排列有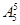 种,然后甲、乙、丙内部再作全排列有
种,然后甲、乙、丙内部再作全排列有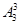 种,故有不同的排法
种,故有不同的排法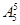
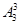 =720种.
=720种.
(3)(插空法)先排甲、乙、丙外的4人有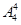 种排法,这四人之间及两端留出五个空位,然后把甲、乙、丙插入到五个空位中有
种排法,这四人之间及两端留出五个空位,然后把甲、乙、丙插入到五个空位中有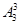 种排法,故共有
种排法,故共有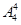
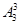 =1440种排法.
=1440种排法.
(4)甲、乙两人有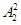 种排法,现从剩下的五人中选一个插入甲、乙中间,有
种排法,现从剩下的五人中选一个插入甲、乙中间,有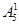 种排法,然后再将这三人看作一个元素,和其他四个元素作全排列,有
种排法,然后再将这三人看作一个元素,和其他四个元素作全排列,有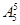 种排法,故共有
种排法,故共有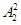
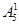
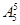 =1200种排法.
=1200种排法.
(5)七个人的全排列为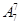 ,其中若只看甲、乙、丙不同顺序的排法有
,其中若只看甲、乙、丙不同顺序的排法有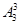 种排法,但只有一种顺序符合要求,故符合要求的不同排法有
种排法,但只有一种顺序符合要求,故符合要求的不同排法有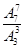 =840种.
=840种.
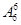 种排法,如果甲站中间5个位置中的一个,而乙不站排尾,则有
种排法,如果甲站中间5个位置中的一个,而乙不站排尾,则有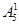
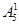
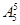 种排法,故共有排法
种排法,故共有排法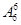 +
+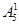
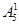
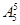 =3720种.
=3720种.方法二(间接法):7个人排成一排有
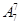 种排法,其中甲在排头有
种排法,其中甲在排头有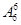 种排法,乙在排尾有
种排法,乙在排尾有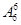 种排法,甲在排头且乙在排尾共有
种排法,甲在排头且乙在排尾共有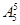 种排法,故共有排法
种排法,故共有排法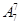 -
-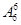 -
-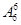 +
+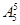 =3720种.
=3720种.(2)(捆绑法)将甲、乙、丙捆在一起作为一个元素与其他4个元素作全排列有
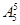 种,然后甲、乙、丙内部再作全排列有
种,然后甲、乙、丙内部再作全排列有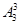 种,故有不同的排法
种,故有不同的排法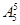
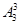 =720种.
=720种.(3)(插空法)先排甲、乙、丙外的4人有
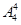 种排法,这四人之间及两端留出五个空位,然后把甲、乙、丙插入到五个空位中有
种排法,这四人之间及两端留出五个空位,然后把甲、乙、丙插入到五个空位中有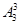 种排法,故共有
种排法,故共有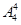
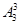 =1440种排法.
=1440种排法.(4)甲、乙两人有
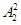 种排法,现从剩下的五人中选一个插入甲、乙中间,有
种排法,现从剩下的五人中选一个插入甲、乙中间,有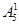 种排法,然后再将这三人看作一个元素,和其他四个元素作全排列,有
种排法,然后再将这三人看作一个元素,和其他四个元素作全排列,有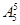 种排法,故共有
种排法,故共有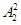
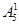
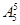 =1200种排法.
=1200种排法.(5)七个人的全排列为
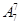 ,其中若只看甲、乙、丙不同顺序的排法有
,其中若只看甲、乙、丙不同顺序的排法有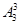 种排法,但只有一种顺序符合要求,故符合要求的不同排法有
种排法,但只有一种顺序符合要求,故符合要求的不同排法有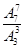 =840种.
=840种.
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
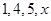 四个不同数字组成四位数,所有这些四位数中的数字的总和为
四个不同数字组成四位数,所有这些四位数中的数字的总和为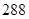 ,则
,则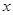 = 。
= 。